16. В треугольнике АВС точка М – середина АС.
А) Докажите, что длина отрезка ВМ больше полуразности, но меньше полусуммы длин
сторон АВ и ВС.
Б) Окружность проходит через точки В, С, М. Найдите хорду этой окружности,
лежащую на прямой АВ, если известно, что АВ=5, ВС=3, ВМ=2.
Пункт А
Итак, отложим от точки M отрезок ME=BM
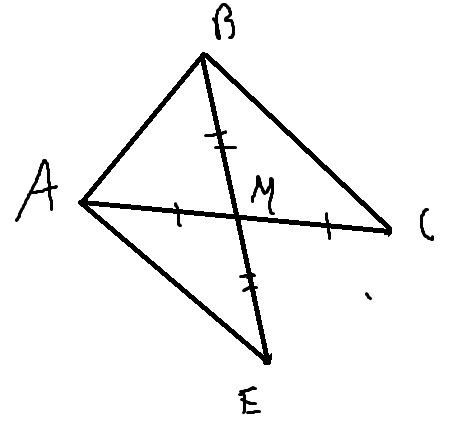
Треугольник \( AME \) равен \( BMC \) (по двум сторонам и углу между ними)
\( AE=BC \)
По теореме о неравенствах треугольника, одна сторона треугольника ABE меньше двух других сторон, запишем это
\( AB<AE+BE \)
Так как AE=BC, а BE=2BM, то
\( AB-BC<2BM \) отсюда \( BM>\frac{AB-BC}{2} \)
Далее применим для EB
\( EB<AB+AE \)
Аналогично (EB=2BM, AE=BC)
\( BM<\frac{AB+BC}{2} \)
Что и требовалось доказать
Пункт Б (если брать наш рисунок, при нахождении хорды получим отрицательное число, что быть не может, поэтому делаем другой рисунок)
Сделаем новый рисунок. (продлим сторону AB, нужно найти хорду BP)
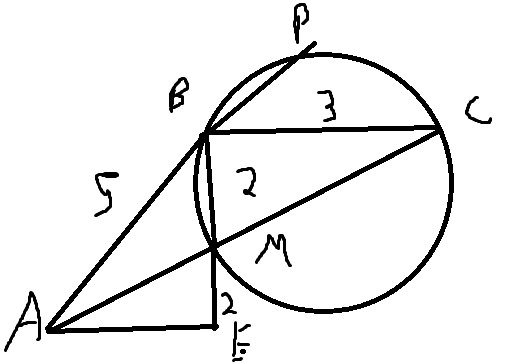
Треугольник ABE-прямоугольный по обратной теореме Пифагора
Тогда угол AEB=90 (AB-гипотенуза)
Углы \( BEA=EBC \) как накрест лежащие
Угол MBC-вписанный и равен 90 градусов, значит MC-диаметр окружности, причем мы его уже может найти по теореме Пифагора
\( MC=\sqrt{4+9}=\sqrt{13} \)
Мы уже доказали равенство треугольников AME и BMC, значит \( AM=MC=\sqrt{13} \)
Применим теорему о секущих
\( AB*AP=AM*AC \)
Пусть BP=х, тогда \( AB*(x+AB)=AM*AC \)
\( 5*(5+x)=\sqrt{13}*2\sqrt{13} \)
\( 5+25x=26 \)
\( x=0.2 \)
BP=0.2
Ответ: 0.2
