16. Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли
точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO=KO.
б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK
составляет 0,09 площади трапеции ABCD.
Решение:
Пункт а
Сделаем рисунок
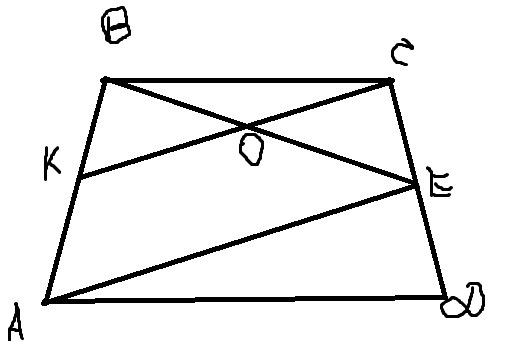
Продолжим сторону BC и AE до пересечения (в точке T) (чтобы увеличить кликните по фотографии)
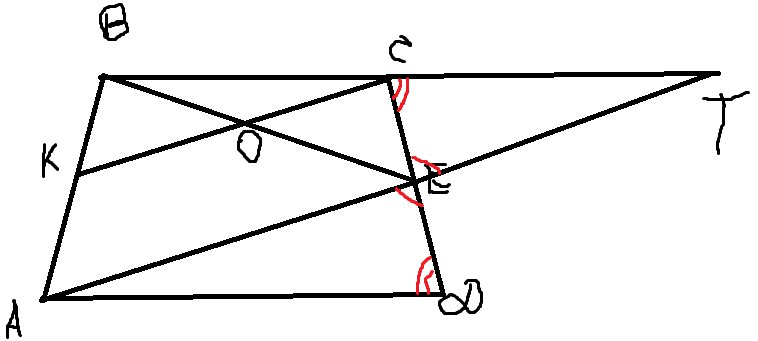
Треугольник \( AED=ECT \)(по стороне и двум прилежащим углам), поэтому \( AE=ET \) Значит BE в треугольнике ABT будет медианой, так как делит сторону пополам. Стороны \( AE \)и \( CK \) параллельны по условию, значит BO-тоже медиана в треугольнике KBC и значит делит сторону пополам. KO=CO что и требовалось доказать.
Пункт б
Заметим, что площадь трапеции равна площади треугольника ABT. Почему? Потому что они состоят из одинаковых частей. Трапеция состоит из \( ABCE+AED \) а треугольник \( ABT \) состоит из тех же частей, значит их площади равны
S-площадь трапеции
\( S=0.09S_{ABT} \)
Отношение площадей равен коэффициенту подобия треугольников.
Треугольник \( KBC \)подобен \( ABT \) (по двум углам) k
K=0.3
\( k=\frac{BC}{BT}=\frac{3}{10} \)
Пусть \( BC=x \) а \( СT=y \)
Тогда \( \frac{x}{x+y}=\frac{3}{10} \)
Выразим отсюда \( x=\frac{3y}{7} \)
Мы доказали, что треугольники \( AED andCET \) равны, значит \( CT=AD \)
Соответственно отношение \( BC \) к \( AD \) равно \( \frac{3}{7} \)
Ответ: \( \frac{3}{7} \)
