16. В остроугольном треугольнике АВС проведены высоты АК, ВМ и СN. На стороне АВ
выбрана точка Р так, что окружность описанная около треугольника РКМ касается
стороны АВ
а) Докажите, что угол КАМ равен углу МВС
б) Найдите РN, если РА = 30, РВ = 10
Решение
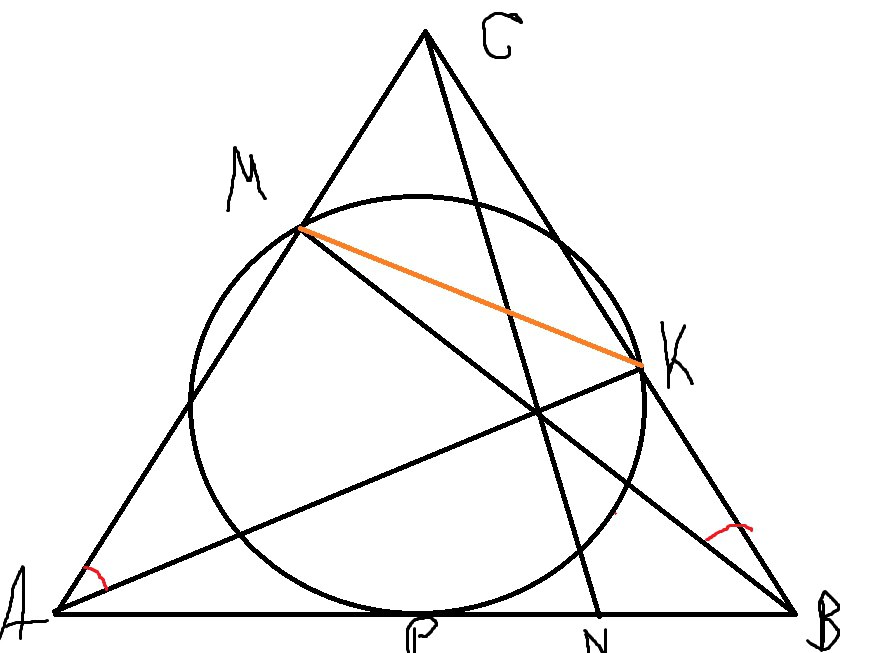
Пункт а достаточно простой, одно подобие.
Итак треугольники \( BMC \) и \( ACK \) подобны по двум углам (Угол C-общий и углы прямые, так как высоты) Если два угла у двух треугольников равны, то и равны все три угла, так как сумма всех углов 180 градусов. На этом пункт а закончен)
Пункт б (самый сложный)
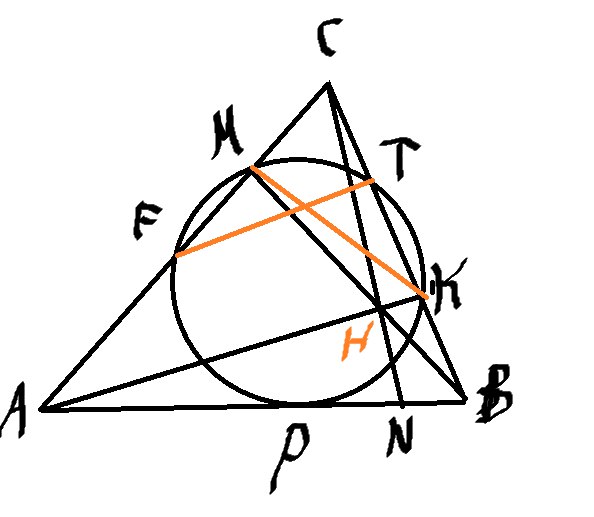
Применим свойство касательной и секущей.
\( BP^2=BK*BT \) (1)
\( AP^2=AF*AM \) (2)
Разделим первое на второе
\( \frac{BP^2}{AP^2}=\frac{BK*BT}{AM*AF} \)
Соединим MK и FT
Углы \( CFT \) = \( MKC \) (так как опираются на одну дугу MT)
Треугольник \( CKM \) подобен \( CFT \) (по двум углам)
Запишем отношение сходственных сторон
\( \frac{CM}{CT}=\frac{CK}{CF} \) или \( \frac{CM}{CK}=\frac{CT}{CF} \)
Треугольник \( CMB \) подобен \( CKA \) (по двум углам, они еще прямоугольные)
\( \frac{CM}{CK}=\frac{CB}{CA} \)
Видим, что одинаковые отношения, значит \( \frac{CT}{CF}=\frac{CB}{CA} \) или \( \frac{CT}{CB}=\frac{CF}{CA} \)
Треугольник \( FTC \) подобен \( ABC \) (по второму признаку), а в подобных треугольниках сотвестнные углы равны. Значит угол \( CFT \) равен углу \( CAB \)
Значит прямые FT и AB параллельны.
Заменим отношение \( \frac{BT}{AF} \) на \( \frac{CT}{CF} \) (это будет одно и тоже по теореме Фалеса)
Заменим \( \frac{CT}{CB} \) на \( \frac{CB}{AC} \)
Треугольники \( AMH \) и \( HKB \) подобны
Значит \( \frac{BK}{AM}=\frac{HK}{HM} \)
Пусть \( PN=x \) тогда \( NB=10-x \)
Треугольники \( CKH \) и \( CNB \) – подобны (по двум углам), запишем отношение сторон
\( \frac{HK}{NB}=\frac{CH}{CB} \) или \( HK*CB=NB*CH \)
Треугольники \( CMH \) и \( CNA \) – подобны (по двум углам, оба прямоугольные)
\( \frac{HM}{AN}=\frac{CH}{AC} \) или \( HM*AC=AN*CH \)
Тогда получим, что \( \frac{BP^2}{AP^2}=\frac{BK*CT}{AM*CF}=\frac{BK*CB}{AM*AC}=\frac{HK*CB}{HM*AC}=\frac{NB*CH}{AN*CH} \)
Получаем, что \( \frac{BP^2}{AP^2}=\frac{NB}{AN} \) подставляем
\( \frac{100}{900}=\frac{10-x}{30+x} \) отсюда находим \( x=6 \)
