Решите неравенство \( 2\sqrt{sin^2x-sinx-1}⩾cos^2x+sinx+3 \)
Решение
Рассмотрим неравенство:
\( \sqrt{f(x)}>g(x) \) – оно равносильно совокупность систем (1) и (2)
(1)\( g(x)<0 \)
\( f(x)⩾0 \)
(2) \( g(x)⩾0 \)
\( f(x)⩾g^2(x) \)
Тут решаем по такому же принципу, сразу обозначим \( sinx=t \), где \( |t|⩽1 \), \( cos^2x=1-t^2 \)
ОДЗ: \( t^2-t-1⩾0 \)
Получаем, что \( t∈[-1;\frac{1-\sqrt{5}}{2}] \)
(1) \( 1-t^2+t+3<0 \)
\( -t^2+t+4>0 \), т.к \( |t|⩽1 \), то получаем, что это выражение истинно при любом t.
Рассматриваем последнее \( f(x)⩾g^2(x) \)
\( 4(t^2-t-1)⩾(-t^2+t+4)^2 \) или \( 4(t^2-t-1)⩾(t^2-t-4)^2 \), т.к квадрат “убивает” минус.
Перепишем чуть в другом виде
\( 4(t^2-t-4+3)⩾(t^2-t-4)^2 \)
Сделаем замену на \( t^2-t-4=z \)
\( 4(z+3)⩾z^2 \)
\( z^2-4z-12⩽0 \)
\( z∈[-2;6] \) и делаем обратную замену
\( -2⩽t^2-t-4⩽6 \)
\( 2⩽t^2-t⩽10 \)
Решаем двойное неравенство, система.
\( t^2-t-2⩾0 \) (1)
\( t^2-t-10⩾0 \) (2)
Если мы пересечем с нашим ОДЗ то получим
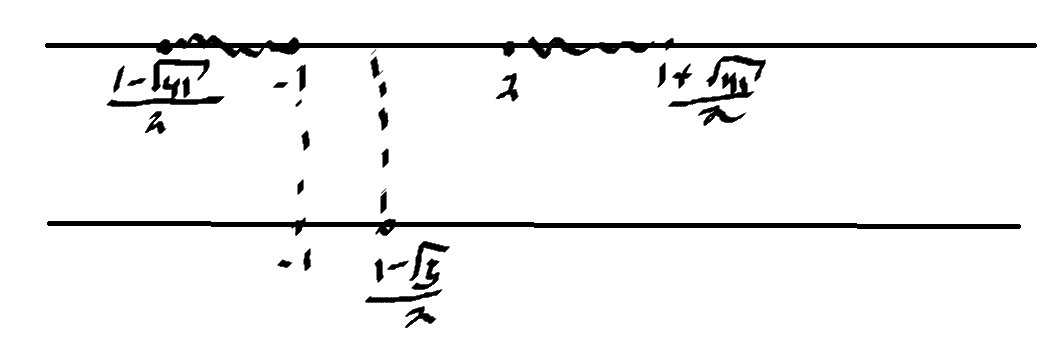
\( t=-1 \)
\( sinx=-1 \)
\( x=-\frac{π}{2}+2πn \) – это ответ)
