Точка M середина ребра AB правильного тетраэдра DABC.
а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.
б) Найдите угол между прямой DM и плоскостью ACD.
Решение
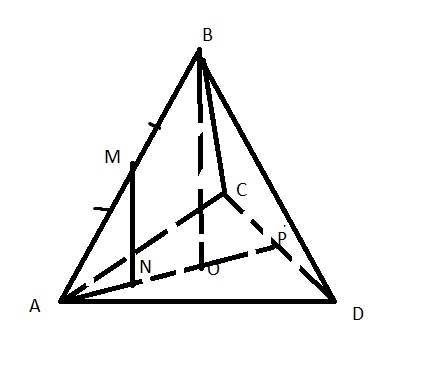
а) В \( △ABP \) проведем \( MN||DO \)
\( BO \) – высота тетраэдра (BO⊥ACD) значит и MN⊥ACD
N-ортогональная проекция т M (она лежит на медиане AP, т.к все построения мы проводили в плоскости ABP) ч.т.д
б)
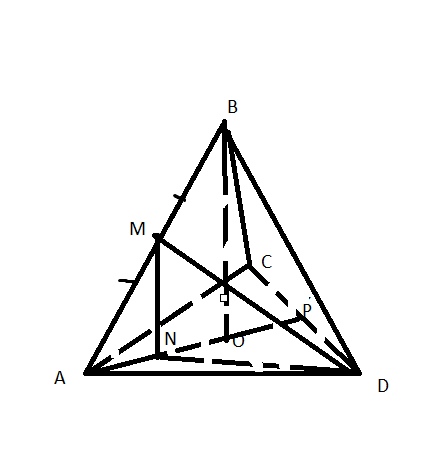
Нам нужно найти угол \( MDN \)
Пусть сторона основания \( a \)
\( DM=\frac{a\sqrt{3}}{2} \) – как высота в равностороннем треугольнике
\( MN=\frac{BO}{2} \)
\( BO=\sqrt{a^2-AO^2} \)
\( AO \) – это радиус описанной окружности \( AO=\frac{a}{\sqrt{3}} \)
\( BO=\frac{a\sqrt{2}}{\sqrt{3}} \)
\( MN=\frac{a\sqrt{2}}{2\sqrt{3}} \)
\( sin∠MDN=\frac{a\sqrt{2}}{2\sqrt{3}}*\frac{2}{a\sqrt{3}}=\frac{\sqrt{2}}{3} \)
Ответ: \( arcsin\frac{\sqrt{2}}{3} \)
