В правильной четырехугольной пирамиде SАВСD сторона основания АВ равна 16, а высота пирамиды равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM = DN = 4 и АК = 3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.
Решение
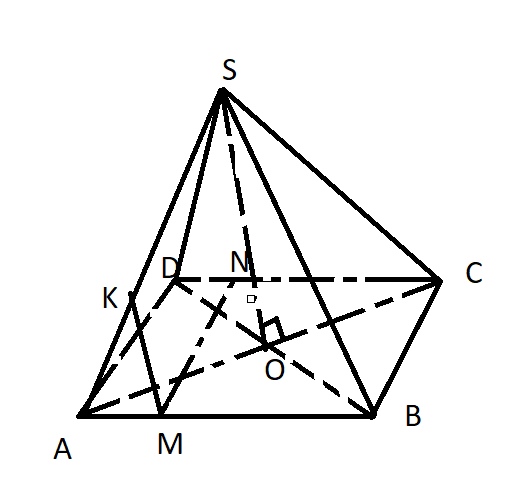
\( AC=16\sqrt{2} \) – как диагональ квадрата
\( AO=OC=8\sqrt{2} \)
По т Пифагора \( AS=12 \)
Заметим, что \( △AKM \) подобен \( △ASB \) по углу и пропорциональным сторонам.
Значит \( KM \) параллельна \( SB \)
Еще конечно же \( MN \) параллельна \( BC \) (т.к точки M и N находятся на одинаковом расстоянии от BC)
Признак параллельности двух плоскостей: если две пересекающихся прямые в одной плоскости параллельны двум пересекающимся прямым в другой плоскости, то эти плоскости параллельны
Собственно первый пункт мы доказали
б) Нам нужно найти расстояние от точки K до пл-ти SBC, но так как плоскости параллельны (из пункта а), то все точки одной плоскости находятся на одинаковом расстояние до другой плоскости, давайте найдем расстояние от точки M до пл-ти SBC (так будет легче и ответ один и тот же).
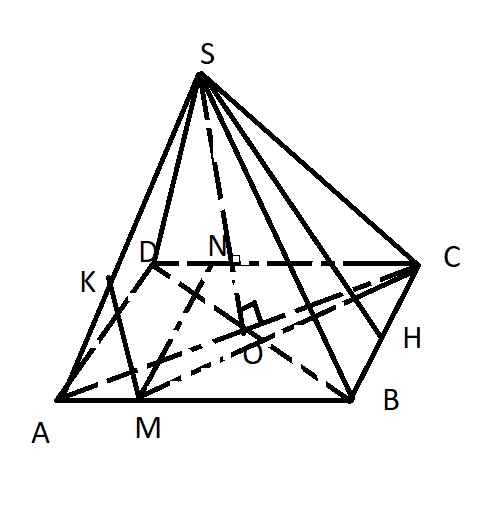
Для этого рассмотрим пирамиду MBCS.
\( V=\frac{1}{3}S_{MBC}*h \)
\( S_{MBC}=0.5*12*16 \) (прямоугольный треугольник)
\( h=SO=4 \)
Но с другой стороны
\( V=\frac{1}{3}*S_{BCS}*h \)
\( S_{BCS}=0.5*BC*SH \)
\( SH=\sqrt{SC^2-HC^2}=\sqrt{12^2-8^2}=\sqrt{80}=4\sqrt{5} \)
\( h \) – это искомое расстояние (перпедикуляр из M на пл-ть SBC)
Мы все записали, осталось только найти \( h \)
Ответ: б) \( \frac{12\sqrt{5}}{5} \)
