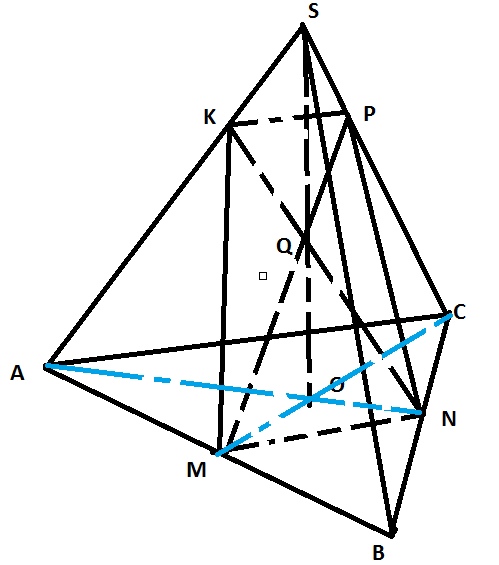
В правильной пирамиде SABC точки M и N –середины ребер АВ и ВС
соответственно. На боковом ребре SA отмечена точка К, SK_KA=1:3. Сечение пирамиды
плоскостью MNK является четырехугольником, диагонали которого пересекаются в
точке Q.
а) Докажите, что точка Q лежит на высоте пирамиды.
б) Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона
основания равна 2, а высота пирамиды равна 4.
Решение
а) Строим сечение: Соединяем \( KM \), т.к точки лежат в одной плоскости, далее т.к \( MN \) – средняя линия, то она параллельная \( AC \) и следовательно всей плоскости \( SAC \), значит плоскость сечения содержит прямую параллельную AC, проведем \( KP∥MN \), соединяем PN, получаем искомое сечение трапецию \( MNKP \)
Так как пирамида правильная, то т \( O \) – центр треугольника основания, т пересечения медиант, высот и биссектрис.
Легко заметить, что пересечение плоскостей \( SAN \) и \( SCM \) дает прямую \( SO \) – высота пирамиды
так как \( KN \) лежит в плоскости \( SAN \), то точка \( Q \) лежит в плоскости SAN
так как \( MP \) лежит в плоскости \( SCM \), то точка \( Q \) лежит в плоскости \( SCM \)
Пересечение прямых \( KN \) и \( MP \) дает точку \( Q \), следовательно\( Q \)
принадлежит обеим плоскостям \( SAN \), \( SCM \), и следовательно лежит на \( SO \)
б) Очевидно, что трапеция равнобедренная по построению. Осталось найти ее высоту, чтобы вычислить площадь сечения, стороны основания находится очень легко.
\( AO=\frac{2}{3}AN=\frac{2\sqrt{3}}{3} \) (AN-легко найти по т Пифагора)
\( AS=\sqrt{SO^2+AO^2}=\frac{2\sqrt{39}}{3} \)
\( cosA=\frac{AM}{AS}=\frac{3}{2\sqrt{39}} \)
\( AK=\frac{3}{4}AS \)
По т косинусов
\( KM=\sqrt{AK^2+AM^2-2AK*AM*cosA}=\frac{\sqrt{37}}{2} \)
Наше сечение трапеция, а равнобедренная она по подобию треугольников AKM и CLN
Мы нашли все стороны трапеции, думаю не составит труда посчитать чему равна ее площадь:)
Ответ: \( \frac{21\sqrt{3}}{16} \)
