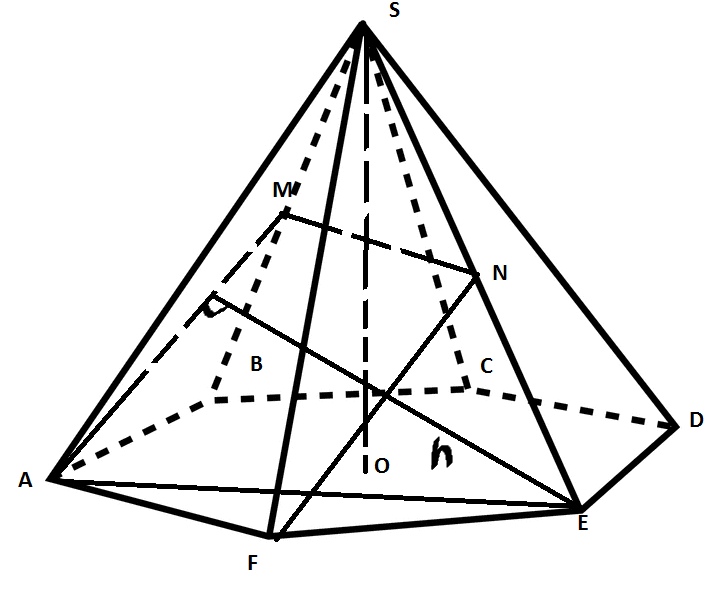
В правильной шестиугольной пирамиде SABCDEF сторона основания АВ=1, высота
SO=2, точка М‐середина ребра BS.
а) Докажите, что АМ параллельна FN, где N – середина ребра SE
б) Найдите расстояние от точки Е до прямой АМ
Решение
а) \( MN \) – средняя линия \( BES \), т.к M и N – середины сторон по условию
\( MN∥BE \), \( BE∥AF \) значит \( MN∥AF \)
\( MN=AF=0,5BE \), значит четырехугольник \( AMNF \) – параллелограмм. и значит \( AM∥FN \)
б) Начнем с конца:
Нам нужно найти \( h \) – высота в треугольника AEM
\( S_{AEM}=0,5AM*h \)
\( S_{AEM}=0,5*AE*sinA \), если найдем синус, то найдем и \( h \)
\( sinA=\sqrt{1-cos^2A} \)
По т косинусов \( cosA=\frac{AM^2+AE^2-EM^2}{2*AM*AE} \) , осталось только все это найти:)
\( AE=\sqrt{3} \) по свойству правильной шестиугольной пирамиды.
\( AO=R=1 \)
\( AS=\sqrt{4+1}=\sqrt{5} \) – по т Пифагора
Вспомним формулу медианы:
\( m_{c}=0,5\sqrt{2a^2+2b^2-c^2} \)
И по ней находим AM и EM – т.к это медианы по условию
\( AM=0,5\sqrt{2AS^2+2AB^2-SB^2}=0,5*\sqrt{2*5+2-5}=\frac{\sqrt{7}}{2} \)
По аналогии
\( EM=\frac{\sqrt{13}}{2} \)
А теперь осталось найти \( cosA \) )) просто подставить
\( cosA=\frac{3}{2\sqrt{21}} \)
\( sinA=\frac{5}{2\sqrt{7}} \)
\( h=AE*sinA=\frac{5\sqrt{3}}{2\sqrt{7}} \)
Ответ: \( h=AE*sinA=\frac{5\sqrt{3}}{2\sqrt{7}} \)
P.S Если понравилось решение или что-то не было понятно, то пиши комментарий ниже, мне будет приятно:)
