В конусе с вершиной в точке Р высота РО=√7 . В его основании проведена
хорда АВ, отстоящая от точки О на расстоянии, равном 3. Известно, что радиус
основания конуса равен 5.
А) Докажите, что расстояние от точки Р до прямой АВ вдвое меньше длины отрезка АВ.
Б) Найдите радиус сферы, описанной около пирамиды РОАВ.
Решение
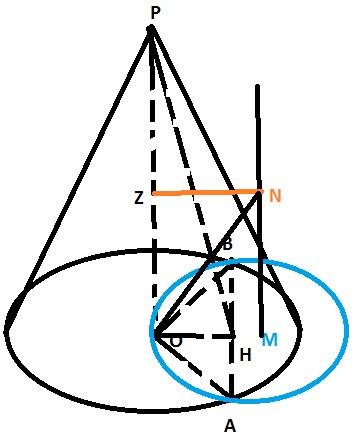
Проведем высоту (\( OH \)) в равнобедренном треугольнике \( ABO \) (она же и биссектриса и медиана)
Проведем и \( PH \)
\( OH \) – проекция прямой \( PH \), а так как \( OH⊥AB \), то по теореме о 3-х перпендикулярах \( PH⊥AB \), и следовательно \( PH \) – это и есть расстояние от \( P \) до \( AB \)
Ну очевидно, что \( AB=8 \), т.к по т. Пифагора (AH=4, египетский треугольник)
Найдем \( PH=\sqrt{PO^2+OH^2}=\sqrt{7+9}=4 \)
\( \frac{AB}{PH}=2 \) ч.т.д.
Б) Для начала нам нужно найти точку, которая равно удалена от точек \( P,O,A,B \)
Опишем окружности вокруг равнобедренного треугольника \( ABO \)
\( R_{ABO}=\frac{5*5*8}{4*0.5*3*8}=\frac{25}{6} \) (\( R=\frac{a*b*b}{4S} \))
Обозначим её центр за \( M \), в итоге точка M – равноудалена от точек \( A,B,O \), но нам этого недостаточно, осталась \( P \)
Построим прямую параллельную \( PO \), построим серединный перпендикуляр к прямой \( PO \), (\( ZN \))
В итоге получаем, что точка \( N \) равноудалена от точек \( P,A,B,O \) – следовательно, это центр сферы.
Найдем радиус по т. Пифагора \( ON=\sqrt{R^2+(0.5PO)^2}=\sqrt{(\frac{25}{6})^2+(\frac{\sqrt{7}}{2})^2}=\frac{2\sqrt{43}}{3} \)
Ответ: \( \frac{2\sqrt{43}}{3} \)
