В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 4, а боковые ребра 5.
а) Докажите, что плоскость A1C1E перпендикулярна плоскости BB1E1
б) Найдите угол между плоскостями A1C1E и ABC.
Решение
Построим первую плоскость (чтобы увеличить кликните по фотке)
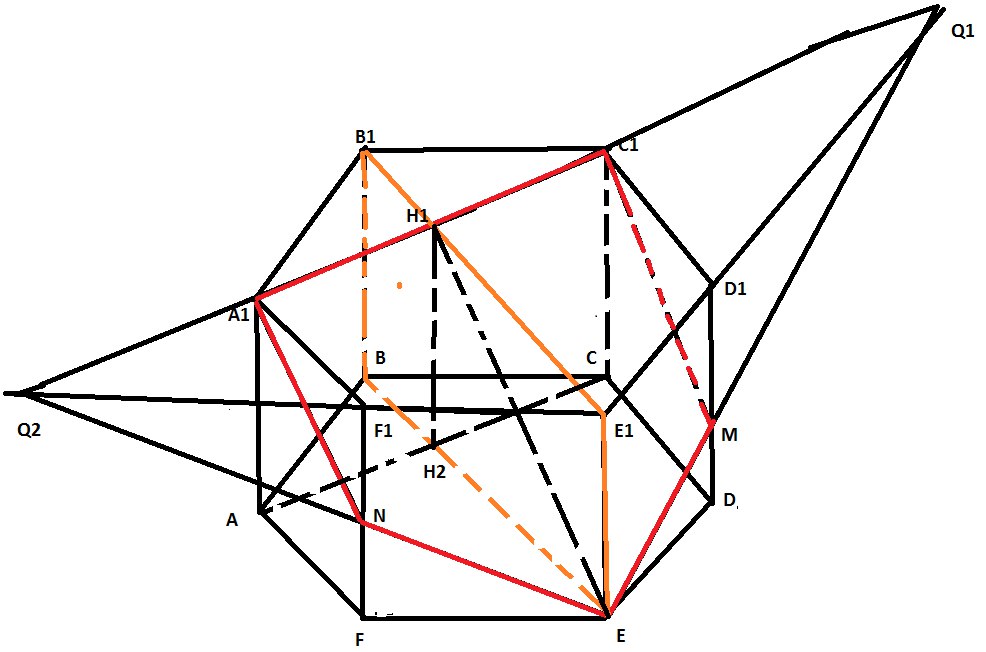
- Соединим A1 и C1, продолжим A1C1 до пересечения с прямой E1D1 в точке Q1
- Соединим Q1 и E, Q1E пересекает DD1 в точке M
- Соединим M и C1
- A1C1 пересекается с прямой E1F1 в точке Q2
- Соединим Q2 и E, Q2E пересекает FF1 в точке N
- Соединим NA1
Со второй плоскостью все легко:
- Соединим B1E1
- Так как плоскости оснований параллельны, то из точки B проведем прямую параллельную B1E1
Искомая плоскость (BB1E1E)
Дополнительно я ввел точку пересечения этих плоскостей H1 и опустил перпендикуляр на основание H1H2. Это нам понадобиться.
А) \( A1C1⊥B1E1 \) (по свойству правильного шестиугольника)
\( A1C1⊥BB1 \)
делаем вывод \( A1C1⊥(BB1EE1) \)
А так как плоскость A1C1E проходим через прямую A1C1, то \( (A1C1E)⊥(BB1EE1) \) ч.т.д.
Б) Можно заметить, что искомый угол между плоскостями ∡H1EH2
\( EH2⊥AC \)
\( EH1⊥A1C1 \) – по т. о 3-х ⊥-ах.
\( HH1=5 \)
нам легче найти тангенс этого угла)
Малая диагональ делит большую в отношение 1:3
\( BE=8 \) большая диагональ равна двум сторонам.
\( BH2=2 \)
\( H2E=6 \)
\( tg∡H1EH2=\frac{5}{6} \)
Ответ: \( arctg\frac{5}{6} \)
