В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ=5, AD=6, AA1=8, точка К –середина ребра DD1
А) Докажите, что прямые ВС и КС1 перпендикулярны.
Б) Найдите отношение объемов, на которые делится прямоугольный параллелепипед
плоскостью ВКС1
Решение
Сделаем рисунок и построим сечение
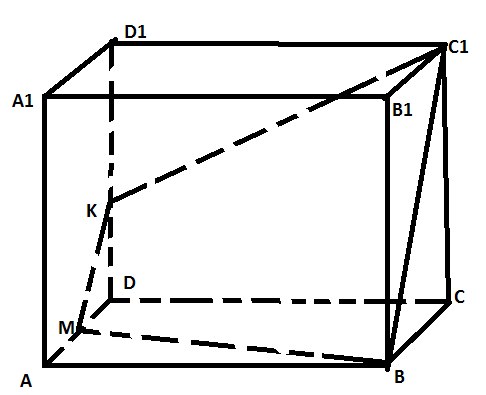
- Соединяем K и С1, B и C1, т.к лежат в одной плоскости
- Из K проводим прямую параллельную BC1 (BB1C1) параллельна (AA1D)
- KM параллельна BC1 (очевидно, что M-середина)
- Соединяем B и M, т. к лежат в одной плоскости
А) \( D_{1}K⊥(A1D1C1) \)
\( D1C1⊥B1C1 \)
по т. о 3-х перпендикулярах \( KC1⊥B1C1 \)
А так как \( B1C1∥BC \), то \( KC1⊥BC \) ч.т.д
Б) \( V=5*6*8=240 \)
\( V_{CC1BMD}=\frac{1}{3}*CC1(S_{DCB}+S_{DMB}) \)
\( S_{DCB}=0.5*DC*BC=0.5*5*6=15 \)
\( S_{DMB}=0.5*S_{ADB}=0.5*0.5*5*6=7.5 \)
\( V_{CC1BMD}=60 \)
\( V_{C1KDM}=\frac{1}{3}*D1C1*S_{KDM}=\frac{1}{3}*5*0.5*3*4=10 \)
\( V_{ост}=240-60-10=170 \)
Ну и отношение \( \frac{17}{7} \)
Ответ: \( \frac{17}{7} \)
