Основанием пирамиды FABCD является квадрат ABCD. На ребре AF взята точка Е
такая, что отрезок СЕ перпендикулярен ребру AF. Проекция О точки Е на основание
пирамиды лежит на отрезке АС и делит его в отношении AO:OC=4:1. Угол ADF равен
900.
А) Докажите, что ребро FC перпендикулярно плоскости основания пирамиды
Б) Найдите разность объемов пирамид FABCD и EABD, если известно, что АВ=1.
Решение
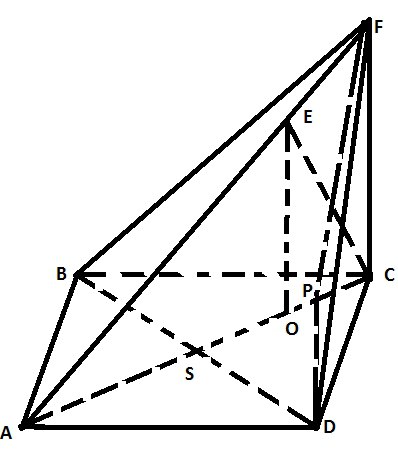
\( EO⊥AC \)
по т. о 3-х перпендикулярах \( AF⊥BD \) (BD⊥AC) – как диагонали квадрата
\( AD⊥CD \), \( AD⊥FD \) – по условию
\( AD⊥(FCD) \), значит \( AD⊥FC \)
если FC не высота пирамиды, то есть какая-то другая высота…
Проведем прямую \( FP⊥AC \)
по т. о 3-х перпендикулярах \( PD⊥AD \), но \( AD⊥CD \), значит точки P и C должны совпадать
Получаем, что \( FC⊥(ADBC) \)
Б)
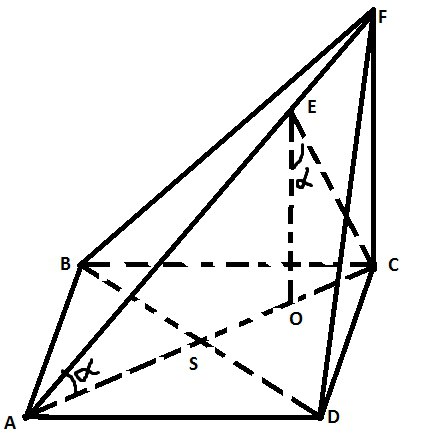
\( AC=BD=\sqrt{2} \)
\( ∡CAF=∡OEC \) – как углы со взаимно перпендикулярными сторонами
\( △AEO \) подобен \( △AFC \) (по 2-м углам)
\( \frac{EO}{FC}=\frac{4}{5} \)
\( EO=\frac{4}{5}FC \)
\( tga=\frac{FC}{AC} \), с другой стороны \( tga=\frac{OC}{EO} \) – приравняем
\( \frac{FC}{AC}=\frac{OC}{EO} \)
\( FC*EO=AC*OC \) (\( OC=\frac{4}{5}\sqrt{2} \)
\( \frac{4}{5}FC^2=\frac{2}{5} \)
\( FC=\frac{\sqrt{2}}{2} \)
\( EO=\frac{4}{5}*\frac{\sqrt{2}}{2} \)
\( V_{FABCD}=\frac{1}{3}*S_{осн}*FC=\frac{1}{3}*1*\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{6} \)
\( V_{EABD}=\frac{1}{3}*\frac{S_{осн}}{2}*EO=\frac{1}{3}*\frac{1}{2}*\frac{4}{5}*\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{15} \)
\( V_{FABCD}-V_{EABD}=\frac{\sqrt{2}}{6}-\frac{\sqrt{2}}{15}=\frac{\sqrt{2}}{10} \)
Ответ: \( \frac{\sqrt{2}}{10} \)
