В правильной шестиугольной пирамиде PABCDEF боковое ребро наклонено к
основанию под углом a=arctg(√3/2)
А) Докажите, что плоскости АРВ и DPE перпендикулярны.
Б) Найдите отношение радиуса сферы, касающейся всех граней пирамиды, к радиусу
сферы, проходящей через все вершины пирамиды
Решение
Сделаем рисунок
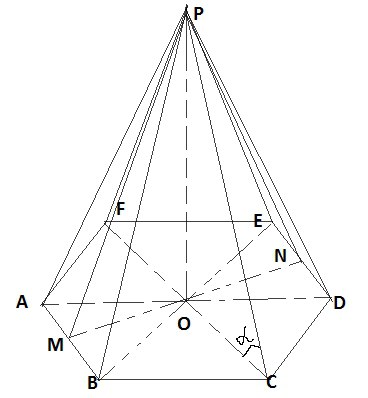
Проведем PM⊥AB и PN⊥ED
Нам нужно доказать, что угол MPE=90 – это и есть угол между плоскостями
Погнали
Обозначим сторону основания пирамиды за \( a \)
По условию \( tga=\frac{PO}{a}=\frac{\sqrt{3}}{2} \)
\( PO=\frac{a\sqrt{3}}{2} \)
\( MO=\frac{a\sqrt{3}}{2} \) – как высота в равностороннем треугольнике.
\( PM=\frac{a\sqrt{6}}{2} \) (по т. Пифагора)
из треугольника PNM (можно сделать выносной чертеж для наглядности)
по т. косинусов
\( 3a^2=3a^2-2*\frac{6a^2}{4}cos∡MPN \)
Находим, что \( cos∡MPN=0 \)
\( ∡MPN=90 \)
значит угол между плоскостями равен 90
б) Пусть r-радиус вписанной сферы
R-радиус описанной сферы
r совпадает с радиусом вписанной окружности в треугольник PMN
R совпадает с радиусом описанной окружности около треугольника PFC
\( S_{PNM}=p_{PNM}*r \)
\( S_{PNM}=0.5*a*\sqrt{3}*\frac{a\sqrt{3}}{2}=\frac{3}{4}a^2 \)
\( p_{PNM}=\frac{a\sqrt{6}+a\sqrt{3}}{2} \)
находим \( r=\frac{1.5a}{\sqrt{6}+\sqrt{3}} \)
По т синусов (обощенной) из треугольника PFC
\( R=\frac{PF}{2sina}=\frac{AP}{2sina} \) (так как AP=PF)
\( AP=\sqrt{AM^2+PM^2}=\frac{a\sqrt{7}}{2} \)
\( tga=\frac{sina}{cosa}=\frac{\sqrt{3}}{2} \) a- острый
\( sina=\frac{\sqrt{3}}{2}*\sqrt{1-sin^2a} \) – возведем в квадрат и выразим
\( sina=\sqrt{\frac{3}{7}} \)
\( R=\frac{6}{7*(\sqrt{2}+1)} \) – это и есть ответ
