В основании пирамиды TABCD лежит трапеция ABCD , в которой ВС||AD и
AD_BC=2. Через вершину Т пирамиды проведена плоскость, параллельная прямой ВС и
пересекающая отрезок АВ в точке М такой, что АМ:MB=2. Площадь получившегося
сечения равна 10, а расстояние от ребра ВС до плоскости сечения равно 4.
А) Докажите, что плоскость сечения делит объем пирамиды в отношении 7:20
Б) Найдите объем пирамиды.
Решение
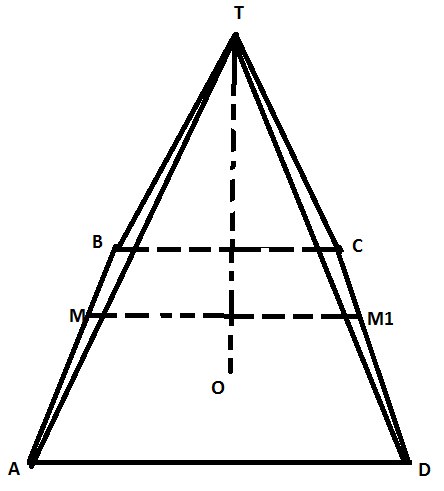
Проводим из точки M прямую параллельную BC и получаем сечение (треугольник) MM1T
а) Сразу же скажем, что высоты этих пирамид совпадают, т.к они имеют общую вершину
\( \frac{V_{TMM_{1}BC}}{V_{TAMM_{1}D}}=\frac{S_{MBCM_{1}}}{S_{AMM_{1}D}} \)
Остается найти площади этих трапеций:)
Сделаем выносной чертеж на плоскость основания, при этом продлим стороны AB и CD до пересечения в точке Z (частый прием в 16)
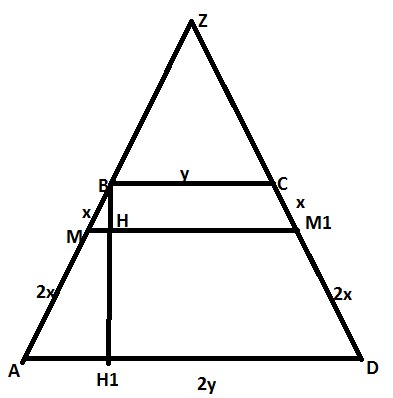
BH1 – высота трапеции.
\( AM=2MB \) по условию, пусть \( MB=x \)
\( AD=2BC \) по условию, пусть \( BC=y \)
из подобия треугольников ZBC и ADZ следует, что \( \frac{ZB}{ZB+3x}=\frac{1}{2} \)
отсюда \( ZB=3x \)
Из подобия треугольников ZBC и MM1Z следует, что \( \frac{y}{MM_{1}}=\frac{3x}{4x} \)
\( MM1=\frac{4}{3}y \)
\( BH=4 \) – по условию, тогда из подобия треугольников MBH и ABH1 следует, что \( \frac{BH}{BH_{1}}=\frac{x}{3x} \)
отсюда \( BH_{1}=12 \), \( HH_{1}=12-4=8 \)
\( S_{AMM_{1}D}=\frac{MM_{1}+AD}{2}*HH_{1}=\frac{\frac{4}{3}y+2y}{2}*8=\frac{40y}{3} \)
\( S_{MBCM_{1}}=\frac{MM_{1}+BC}{2}*4=\frac{\frac{4}{3}y+y}{2}*4=\frac{14y}{3} \)
\( \frac{V_{TMM_{1}BC}}{V_{TAMM_{1}D}}=\frac{S_{MBCM_{1}}}{S_{AMM_{1}D}} =\frac{14y}{40y}=\frac{7}{20} \)
Б) Нам нужно как-то использовать площадь сечения…
\( V=V_{TMM_{1}BC}+V_{TAMM_{1}D}=\frac{27}{7}V_{TMM_{1}BC} \) (из пункта а)
V-объем всей пирамиды
\( \frac{V_{TMM_{1}BC}}{V_{TMBM_{1}}}=\frac{S_{BMM_{1}C}}{S_{BMM_{1}}} \)
\( S_{BMM_{1}}=0.5*MM_{1}*4=\frac{8}{3}y \)
\( S_{BCMM_{1}}=\frac{14}{3}y \)
\( \frac{V_{TMM_{1}BC}}{V_{TMBM_{1}}}=\frac{S_{BMM_{1}C}}{S_{BMM_{1}}}=\frac{7}{4} \)
\( V_{TMM_{1}BC}=\frac{7}{4}V_{TMBM_{1}}=\frac{7}{4}*\frac{40}{3}=\frac{70}{3} \)
\( V_{TMBM_{1}}=\frac{1}{3}*S_{MM_{1}T}*4=\frac{40}{3} \)
\( V=\frac{27}{7}*\frac{70}{3}=90 \)
Ответ: 90
