На боковых ребрах DB и DC треугольной пирамиды ABCD расположены точки М и
N так, что ВМ=MD и CN:ND=2:3. Через вершину А основания пирамиды и точки М и N
проведена плоскость, пересекающая медианы боковых граней, проведенные из
вершины D, в точках К, R и Т.
А) Докажите, что площадь треугольника KTR составляет 5/22 от площади сечения
пирамиды плоскостью
Б) Найти отношение объемов пирамид KRTC и ABCD.
Решение
С построением сечения проблем возникнуть не должно, просто соединяем точки, которые лежат в одной плоскости.
Мы будем пользоваться теоремой Менелая и свойством: если два треугольника имеют общий угол, то их площади относятся как произведение сторон, содержащих этот угол.
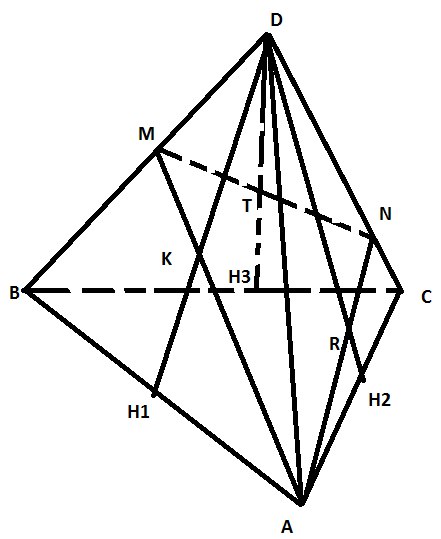
Рассмотрим грань \( ADC \) и применим теорему Менелая (можно сделать выносной чертеж для лучшего понимания)
\( \frac{CH_{2}}{H_{2}A}*\frac{AR}{RN}*\frac{DN}{DC}=1=\frac{AR}{RN}*\frac{3}{5} \) отсюда
\( \frac{AR}{RN}=\frac{5}{3} \)
\( \frac{AK}{KM}=\frac{2}{1} \) – по свойству медианы
Рассмотрим грань \( DBC \) для нее я сделаю выносной чертеж
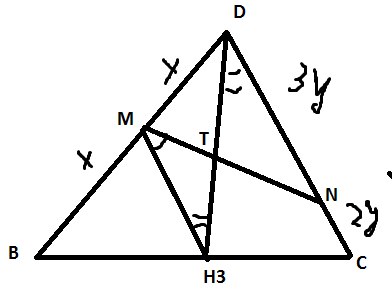
Проведем MH3, заметим, что MH3-средняя линия, значит она равна половине основания то есть 2.5y
запишем подобие треугольников \( MTH_{3} \) и \( TND \)
\( \frac{MH_{3}}{DN}=\frac{MT}{TN}=\frac{5}{6} \)
Сделаем выносной чертеж на \( AMN \)
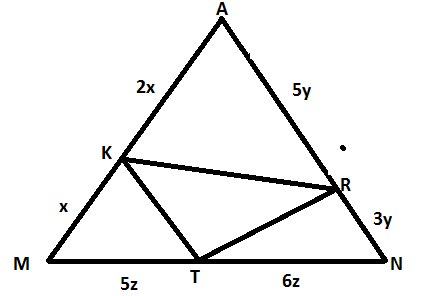
Пользуемся свойством: если два треугольника имеют общий угол, то их площади относятся как отношение длин сторон, содержащих этот угол.
\( S_{AKR}=\frac{2x}{3x}*\frac{5y}{8y}*S_{AMN}=\frac{5}{12}S_{AMN} \)
\( S_{AKT}=\frac{x}{3x}*\frac{5z}{11z}*S_{AMN}=\frac{5}{33}S_{AMN} \)
\( S_{RNT}=\frac{3y}{8y}*\frac{6z}{11z}S_{AMN}=\frac{18}{88}S_{AMN} \)
\( S_{KRT}=S_{AMN}-(S_{AKR}+S_{AKT}+S_{RNT}) \)
\( S_{RKT}=S_{AMN}(1-(\frac{5}{12}+\frac{5}{33}+\frac{18}{88}))=\frac{5}{22}S_{AMN} \) ч.т.д
б) \( \frac{V_{KRTC}}{V_{CMNA}}=\frac{S_{KTR}}{S_{MNA}}=\frac{5}{22} \) (так как у них одинаковые высоты)
Пусть \( V_{DABC}=V \)
\( V_{CAMN}=V-V_{MABC}-V_{DAMN} \)
\( V_{MABC}=0.5V \) (так как одинаковые основания, но высота в два раза меньше)
\( \frac{V_{DMNA}}{V}=\frac{DA}{DA}*\frac{DM}{DB}*\frac{DN}{DC}=\frac{3}{10} \) (как пирамиды с общим трехгранным углом)
\( V_{CAMN}=V-0.5V-0.3V=0.2V \)
\( \frac{V_{KRNC}}{V}=\frac{\frac{5}{22}*0.2V}{V}=\frac{1}{22} \) – это ответ.
