Куб целиком находится в правильной треугольной пирамиде SABC с вершиной S
так, что одна грань куба принадлежит основанию, одно ребро целиком принадлежит
грани SBC, а грани SAB и SAC содержат по одной вершине куба. Известно, что ребро АВ
в 2 раза больше высоты пирамиды.
А) Докажите, что плоскость, проходящая через вершины куба, принадлежащие граням
SAB и SAC, и вершину пирамиды, перпендикулярна плоскости ASD, где D – середина
стороны ВС.
Б) Найдите отношение объемов пирамиды и куба.
Решение
Сделаем рисунок, проведем плоскости \( SAD \) и \( STP \) (нам нужно доказать, что они перпендикулярны)
Так же построим высоту пирамиды \( SO_{1} \) она пересекает верхнюю грань куба в точке \( O_{2} \)
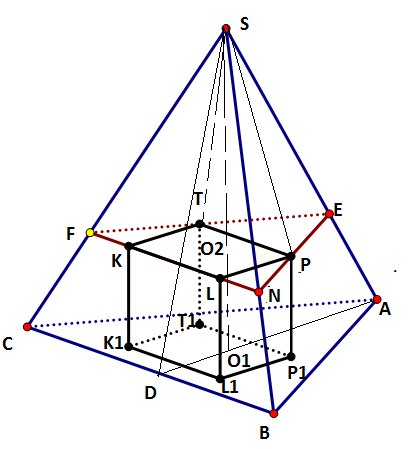
Противоположные плоскости куба параллельны. \( (KTP)∥(K_{1}T_{1}P_{1}) \)
Если две плоскости пересечены третьей, то линии их пересечения параллельны. Получаем, что \( FN∥BC \), а так как KL лежит на FN, то и \( KL∥BC \) значит и \( TP∥BC \)
Получаем, что \( BC∥(STP) \) (\( TP∥BC \))
SD и AD -высоты и медианы в соответствующих треугольниках. \( BC⊥SD \), \( BC⊥AD \).
Делаем вывод, что \( BC⊥(ASD) \), так как BC ⊥ двум пересекающимся прямым лежащих в этой плоскости.
А так как \( BC∥(STP) \), то \( (STP)⊥(ASD) \)
Погнали дальше
Б) Обозначим высоту пирамиды за \( h \)
\( AB=2h \) – по условию
\( V_{п}=\frac{1}{3}*S_{осн}*h=\frac{\sqrt{3}*h^3}{3} \)так как\( S_{осн}=0.5*2h*2h*sin60=\sqrt{3}h \)
Чтобы получить искомое отношение, нужно выразить ребро куба как-то через \( h \) к этому и будет идти)
Обозначим сторону куба за \( a \)
Заметим, что так как \( FN∥BC \) (аналогично по пункту а \( NE∥AB \), \( FE∥AC \))
\( △FNE \) подобен \( △ACB \)(по двум углам) , значит \( △FNE \) – равносторонний.
\( △TEP \) подобен \( △FNE \)(по двум углам) (по той же причине) – следовательно он равносторонний.
\( TP=TE=PE=a \)
из прямоугольного треугольника \( △NO_{2}P \) получаем, \( sin60=\frac{O_{2}P}{NP} \)( \( ∡O_{2}NP=60 \) ), значит \( NP=\frac{a*2}{\sqrt{3}} \)
\( NE=NP+PE=\frac{a*2}{\sqrt{3}}+a \)
Теперь возможно совсем не очевидная вещь. \( O_{2}O{1}=a \) - так как это расстояние между плоскостями оснований, \( SO_{2}=h-a \)
\( △SO_{2}N \)подобен \( △SO_{1}B \)(по двум углам)\( \frac{SN}{SB}=\frac{SO_{2}}{SO_{1}}=\frac{h-a}{h} \)
Очевидно, что \( △SNE \) подобен \( △SAB \), значит \( \frac{NE}{AB}=\frac{SN}{SB}=\frac{h-a}{a} \) отсюда \( NE=2h*\frac{h-a}{h}=2(h-a) \)
теперь приравняем \( 2(h-a)=\frac{2a}{\sqrt{3}}+a \) отсюда \( a=\frac{2h*\sqrt{3}}{2+\sqrt{3}} \)
\( V_{к}=a^3 \)
\( \frac{V_{п}}{V_{к}}=\frac{(2+\sqrt{3})^3}{72} \) – это ответ:)
