Основание пирамиды DABC —прямоугольный треугольник ABC с прямым углом C.
Высота пирамиды проходит через середину ребра AC, а боковая грань ACD—
равносторонний треугольник.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и
произвольную точку M ребра AD,—прямоугольный треугольник.
б) Найдите расстояние от вершины D до этой плоскости, если M — середина ребра AD,
а высота пирамиды равна 6.
Решение
Сделаем рисунок
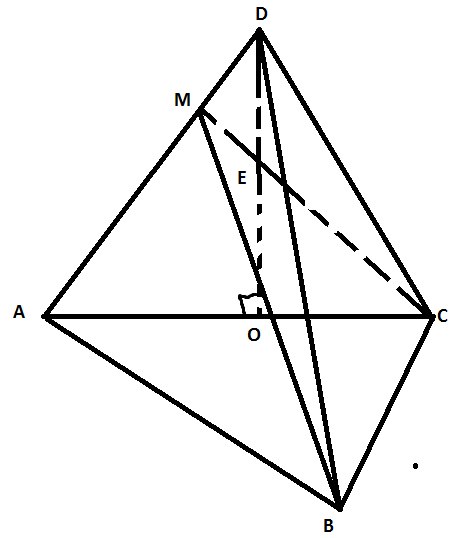
а) B и M, C и M мы соединяем, т.е лежат в одной плоскости, и получаем сечение – треугольник \( BMC \)
\( DO⊥(ABC) \), \( AC⊥(BC) \) – по условию
\( EO \) – высота, \( EC \) – наклонная, \( OC \) – проекция,
Так как \( OC⊥BC \), то по т о 3-х перпендикуляр, \( EC⊥BC \)
Получаем, что треугольник \( MCB \) – прямоугольный, с прямым углом \( ∡MCB=90 \)
б) \( BC⊥CM \) и \( BC⊥AC \), значит \( BC⊥(ADC) \), т.к она перпендикулярна к двум пересекающимся прямым.
По условию треугольник \( ADC \) – равносторонний, \( CM \) – высота и медиана.
\( CM⊥DM \), и \( BC⊥DM \), делаем вывод, что \( DM⊥(MCB) \) – значит искомое расстояние
\( DM \)
Сделаем выносной чертеж
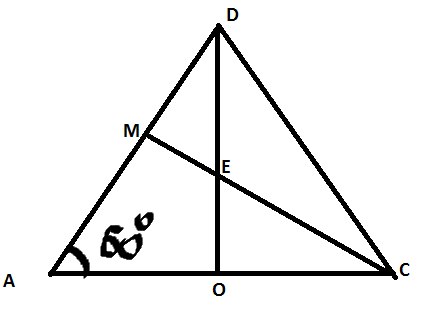
\( sin60=\frac{DO}{AD} \)
\( AD=\frac{DO}{sin60}=\frac{12}{\sqrt{3}} \)
\( DM=0.5AD=\frac{6}{\sqrt{3}}=2\sqrt{3} \)
Ответ: \( 2\sqrt{3} \)
