В кубе ABCDA1B1C1D1 точка О1 – центр квадрата АВСD, точка О2 – центр
квадрата СС1D1D.
а) Докажите, что прямые А1О1 и В1О2 – скрещивающиеся.
б) Найдите расстояние между прямыми А1О1 и В1О2, если ребро куба равно 2
Решение
А) Нарисуем куб и прямые A1O1 и B1O1, проведем диагональное сечение \( AA1CC1 \), в котором лежит наша прямая A1O1.
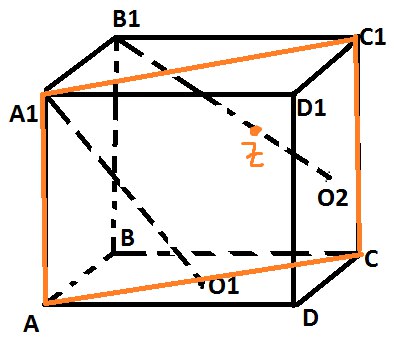
Прямая B1O2 пересекает плоскость в какой-то точке, назовем \( Z \)
B1O2 не лежит в плоскости \( AA1CC1 \)
По теореме прямые B1O1 и A1O1 скрещивающиеся : Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Б) Находим расстояние между скрещивающимися прямыми, по известному нам способу (сто раз делали в 14 задаче). Расстояние между скрещивающимися прямыми – это расстояние от первой прямой до параллельной ей плоскости, целиком содержащей вторую прямую.
Построим из точки B1 прямую B1K параллельную прямой A1O1
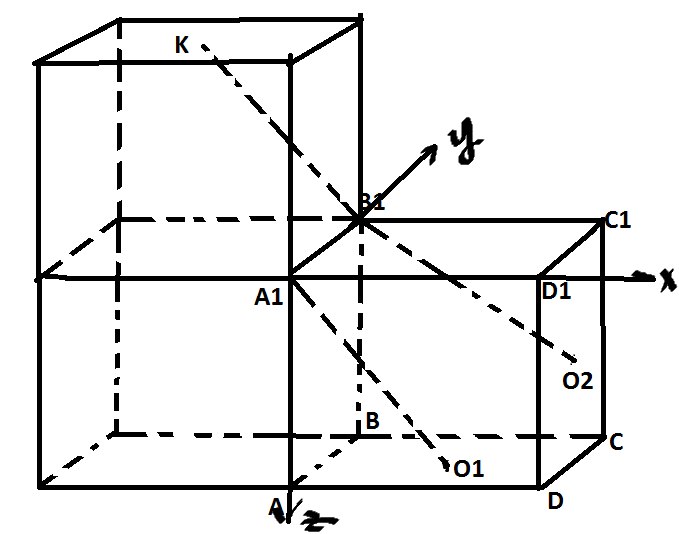
Получается, что нам нужно найти расстояние от точки A1 до плоскости \( KB1O2 \)
\( K(-1;1;-2) \)
\( A1(0;0;0) \)
\( B1(0;2;0) \)
\( O2(2;1;1) \)
Уравнение плоскости \( ax+by+cz+1=0 \)
Подставим координаты точки B1
\( 2b+1=0 \) значит \( b=-0,5 \)
Подставим координаты точки O2
\( 2a+b+c+1=0 \), \( 2a-0.5+c+1 =0\), \( c=-2a-0,5 \)
Подставляем координаты K точки K
\( -a+b-2c+1=0 \), \( a=-0,5 \) значит \( c=0,5 \)
\( d(A1;KB1O2)=\frac{1}{\sqrt{\frac{1}{4}+\frac{1}{4}+\frac{1}{4}}}=\frac{2\sqrt{3}}{3} \)
Ответ: \( \frac{2\sqrt{3}}{3} \)
