В одном основании прямого кругового цилиндра с высотой 12 и радиусом
основания 6 проведена хорда AB, равная радиусу основания, а в другом его основании
проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее
через прямую AB перпендикулярно прямой CD так, что точка C и центр основания
цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
Решение
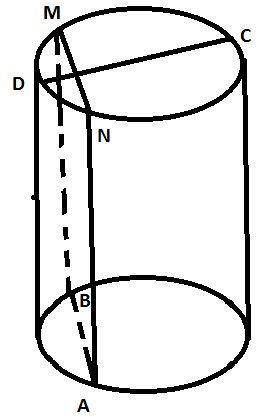
Так как плоскость сечения пересекает две параллельные плоскости, то линии пересечения плоскостей будут параллельными, т.е AB параллельна MN.
Пункт А, на самом деле очень простой. Прямая CD перпендикулярна плоскости ABNM
\( (DMC)⊥(MNAB) \) – т.к Если плоскость проходит через прямую, перпендикулярную другой плоскости, то такие плоскости взаимно перпендикулярны.
\( AB=MN \) – это в принципе и так очевидно, т.к MN – проекция AB на плоскость основания, но можно доказать строго с помощью равенства соответствующих треугольников.
\( AN \) и \( BN \) – образующие цилиндра, значит они перпендикулярны плоскостям основания, в том числе прямой AB
\( ABNM \) – прямоугольник. А по свойству прямоугольника : его диагонали равны.
Пункт Б
\( V=\frac{1}{3}*S_{осн}*h \)
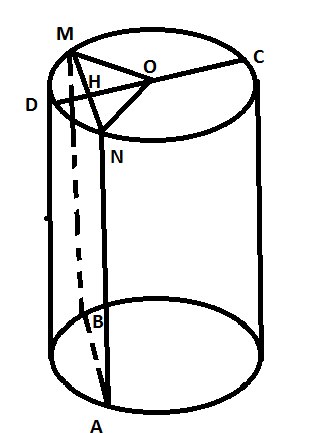
По условию \( DC⊥AB \) и еще \( DC⊥AN \) значит \( DC⊥(ABNM) \)
Вывод: \( CH \) – высота пирамиды
треугольник \( MON \) – равносторонний, так как по условию сторона равна радиусу.
\( OH=\frac{6\sqrt{3}}{2}=3\sqrt{3} \) – как высота правильного треугольника.
\( CH=6+3\sqrt{3} \)
\( S_{осн}=MN*AN=12*6 \)
\( V=\frac{1}{3}*12*6*(6+3\sqrt{3})=144+72\sqrt{3} \)
