Основание и высота правильной треугольной призмы ABCA1B1C1 равны AB =6, AA1=4.
а) Найдите угол между прямыми A1B и B1C
б) Найдите расстояние между прямыми A1B и B1C
Решение
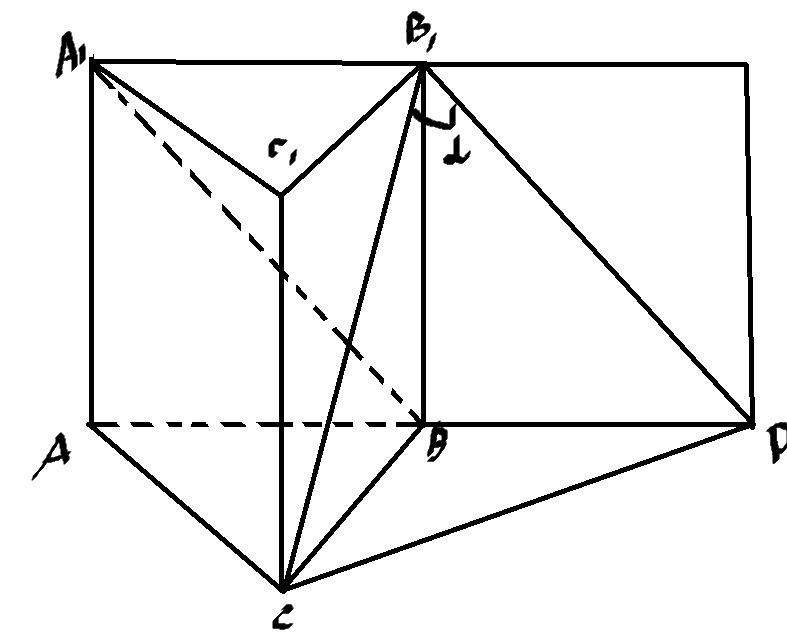
Задача слишком тривиальная, поэтому подробно расписывать не стал.
Построим плоскость параллельную прямой A1B, при этом прямая B1P будет равна и параллельна A1B.
Искомый угол CB1P=a.
\( ∡ABC=60 \), \( ∡CBP=120 \), \( ∡BCP=∡BPC=30 \) (так как треугольник BCP-равнобедренный, AB=BP)
Получаем, что треугольник ACP- прямоугольный (60+30=90)
\( CP=\sqrt{AP^2-AC^2}=\sqrt{144-36}=2\sqrt{27} \).
\( CB1=B1P=\sqrt{36+16}=\sqrt{52} \)
Из треугольника B1CP по т косинусов имеем:
\( CP^2=CB1^2+B1P^2-2CB1*PB1*cosa \) отсюда \( cosa=-\frac{1}{26} \), значит \( a=π-arccos(1/26) \)
б) Расстояние между скрещивающимися прямыми – это расстояние от первой прямой до параллельной ей плоскости, целиком содержащей вторую прямую. Искомое расстояние равно высоте пирамиды BB1CP, обозначим его за h
\( V_{BCPB1}=1/3*h*S_{CPB1} \), и \( S_{CPB1}=0.5*B1H*CP=0.5\sqrt{4*13-27}*2*\sqrt{27}=5\sqrt{27} \)
\( V_{B1BCP}=1/3*BB1*S_{BCP} \), и \( S_{BCP}=0.5*CB*BP*sin120=9\sqrt{3} \)
\( V_{BCPB1}=V_{B1BCP} \), значит \( h=2.4 \)
Ответ: 2,4
