В параллелепипеде ABCDA1B1C1D1 точка К – середина ребра АВ.
а) Докажите, что плоскость СКD1 делит объем параллелепипеда в отношении 7:17.
Б) Найдите расстояние от точки D до плоскости СКD1, если известно, что ребра АВ, АD и
АА1 попарно перпендикулярны и равны соответственно 6, 4 и 6.
Решение
Сделаем рисунок
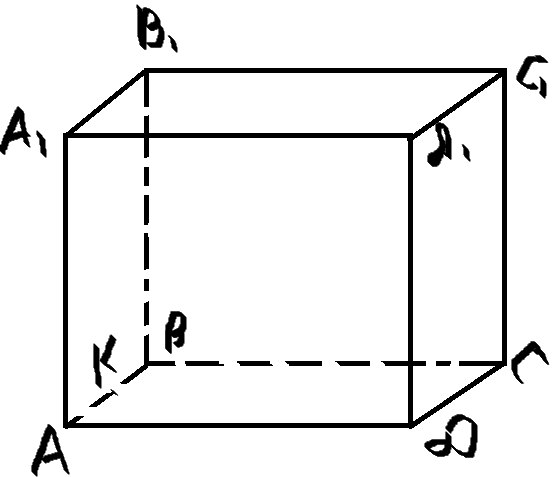
Строим сечение:
- Соединим C и D1, С и K, так как они лежат в одной плоскости
- Так как плоскость сечения пересекает две грани, которые параллельны, то линии пересечения плоскостей будут параллельными. Построим из точки K прямую параллельную D1C, и обозначим пересечение с ребром AA1 точкой P
- Соединим P и K, так как они лежат в одной плоскости
Сечение мы построили (я дополнительно ввел систему координат, чтобы сто раз рисунок не перерисовывать, это для пункта Б) (кликните, чтобы увеличить)
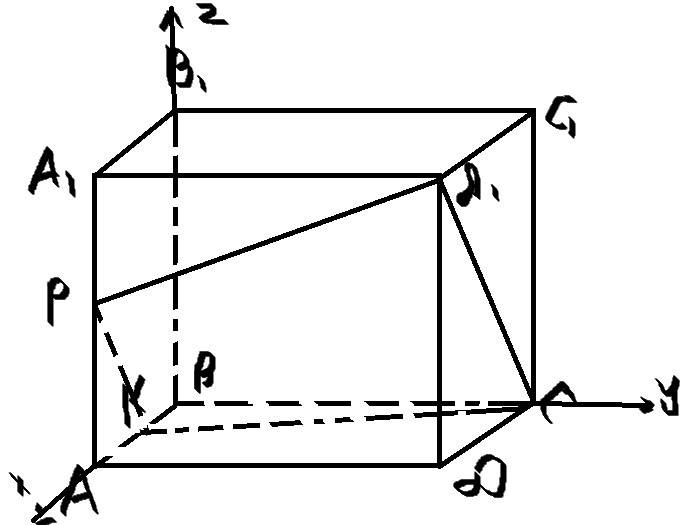
Пункт А
\( V_{ABCDA1B1C1D1}=S_{DD1CC1}*h \) (основанием не обязательно является ABCD)
Пусть \( S_{DD1CC1}=S_{осн} \) (это я чтобы удобнее писать было)
Сечение разбивает параллелепипед на две части, переднюю и заднюю. Найдем объем передней УСЕЧЕННОЙ пирамиды, по формуле.
\( V_{APKDD1C}=\frac{1}{3}*h*(S_{APK}+\sqrt{S_{APK}*S_{DD1C}}+S_{DD1C}) \)
Заметим, что треугольники PKA и DD1C подобны по двум углам, значит их площади относятся как квадрат коэффициент подобия ( он равен 1/2, так как K-середина)
Заметим, что \( S_{DD1C}=0.5*S_{осн} \)
\( \frac{S_{APK}}{S_{DD1C}}=\frac{1}{4} \)
отсюда \( S_{APK}=\frac{S_{DD1C}}{4}=\frac{S_{осн}}{8} \)
Теперь подставляем все в формулу объема
\( V_{APKDD1C}=\frac{1}{3}*h(\frac{S_{осн}}{8}+\sqrt{\frac{S_{осн^2}}{16}}+\frac{S_{осн}}{2})=S_{осн}*h*\frac{7}{24} \)
Значит оставшаяся часть \( V_{ост}=S_{осн}*h-S_{осн}*h*\frac{7}{24}=\frac{17}{24}S_{осн}*h \)
Ну если поделим одно на другое то и получим искомое отношение…
Пункт Б
Вводим прямоугольную систему координат и находит уравнение плоскости сечения, а далее находим искомое расстояние по известной нам формуле
B(0;0;0), K(3;0;0), C(0;4;0), D1(6;4;6)
ax+by+cz+d=0 – уравнение плоскости
Дальнейшее решение на листочке (чтобы увеличить,клинките по фотографии)

Ответ: \( \frac{24\sqrt{41}}{41} \)
