14. В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ=ВС=4, СС1=8. Точка К –середина ребра АВ, точка М – середина ребра ВС. Точка Р лежит на ребре DD1 так,
что DP:PD1=3:5.
А) Докажите, что плоскость КМР перпендикулярна прямой DВ1.
Б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда
плоскостью КМР, а вершиной – точка D.
Решение
Для начала построим сечение, изображаем прямоугольный параллелепипед. И строим по шагам:)
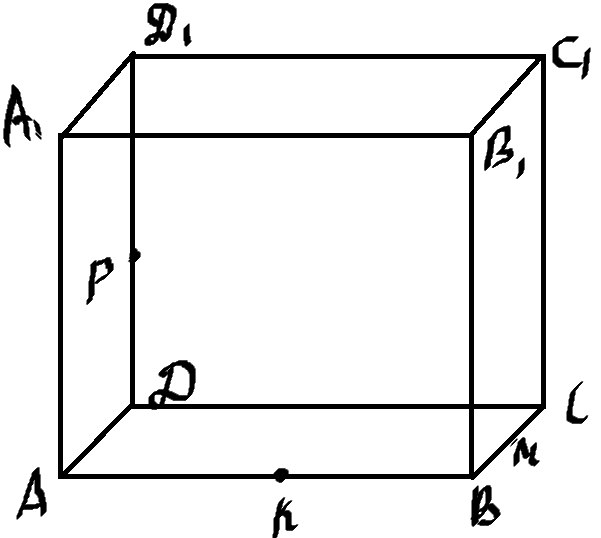
- Соединяем K и M, так как лежат в одной плоскости (ABC)
- Продолжаем отрезок KM до пересечения с прямой AD и DC
- Точки пересечения обозначим Q1 и Q2 соотвественно
- Соединяем Q1 и P, так как они лежат в одной плоскости, точку пересечения прямой Q1P с ребром AA1 обозначим L
- Соединяем Q2 и P, так как лежат в одной плоскости, точку пересечения прямой Q2P с ребром CC1 обозначим Z
- Соединяем KL и ZM, так как лежат в одной плоскости
- Итак получили сечение \( KLPZM \) (чтобы увеличить кликните по фотографии)
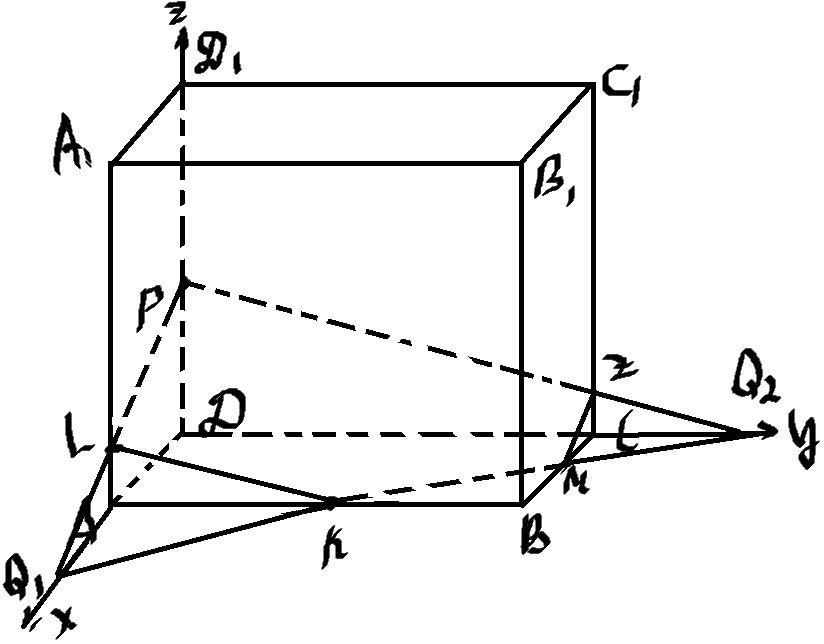
Главное дело сделали, поехали дальше)
Пункт А
Введем прямоугольную систему координат с началом D(0;0;0)
Итак поясню что мы будем делать. Я составлю уравнение плоскости \( KMP \) и найду вектор нормали, если он будет параллелен вектору DB1, то собственно DB1 будет перпендикулярно плоскости сечения
Приступим.
Координаты точек найти не составляет труда (если у вас трудности, то пишите комментарии, я все объясню)
\( P(0;0;3) \) , \( M(2;4;0) \), \( K(4;2;0) \) – теперь составим уравнение плоскости
Доказательство на фотографии (чтобы увеличить, клинките по фотке)

Пункт Б
Площадь сечения искать достаточно трудно без векторного метода….
Площадь сечения равна площади проекции этого сечения на плоскость основания деленное на косинус угла между плоскостями. Это известная теорема, ее доказывать не нужно.
\( S_{KMP}=\frac{S_{проекция}}{cosa} \)
Осталось найти угол и площадь проекции а точнее \( S_{KMCDA} \)
Найдем \( S_{KMCDA}=S_{ABCD}-S_{KMB} \) это сделать очень легко, даже не буду тратить место на это. (треугольник KMB-прямоугольный, а ABCD-квадрат, все известно)
\( S_{KMCDA}=14 \)
Найдем теперь косинус между двумя плоскостями.
\( cosa=\frac{x_{1}*x_{2}+y_{1}*y_{2}+z_{1}*z_{2}}{\sqrt{x_{1}^2+y_{1}^2+z_{1}^2}*\sqrt{x_{2}^2+y_{2}^2+z_{2}^2}} \)
Где x1 y1 z1 – координаты вектора нормали n
А x2 y2 z2 – координаты вектора нормали плоскости проекции пусть будет N
Координаты n-мы уже знаем, а координаты N(0;0;1) – вектор перпендикулярный плоскости основания
Находим косинус угла
\( cosa=\frac{1*0+1*0+2*1}{\sqrt{1+1+4}*\sqrt{1}}=\frac{\sqrt{6}}{3} \)
\( S_{KMP}=\frac{14*3}{\sqrt{6}}=7\sqrt{6} \)
\( V_{PQ_{1}DQ_{2}}=1/3*S_{Q_{2}DQ_{1}}*DP=1/3*0.5*6*6*3=18 \)
\( V_{ZDMQ_{2}}=1/3*S_{MDQ_{2}} *CZ=2\)
\( V_{иск}=V_{PQ_{1}DQ_{2}}-2V_{ZDMQ_{2}}=14 \)
Ответ: 14
