14. В правильной треугольной пирамиде SABC точка К – середина ребра АВ. На ребре SC взята точка М так, что SM : СМ = 1:3.
а) Докажите, что прямая МК пересекает высоту SО пирамиды в её середине.
б) Найдите расстояние между прямыми МК и АС, если известно, что АВ=6, SA=4.
Пункт А
Решение
Пункт Б
Я решил сделать два способа решения
Первый способ смотрите по ссылке gdz-larin.ru/?p=758
Сделаем чуть чуть другой рисунок, чтобы было лучше видно (высоту пирамиды я специально скосил)
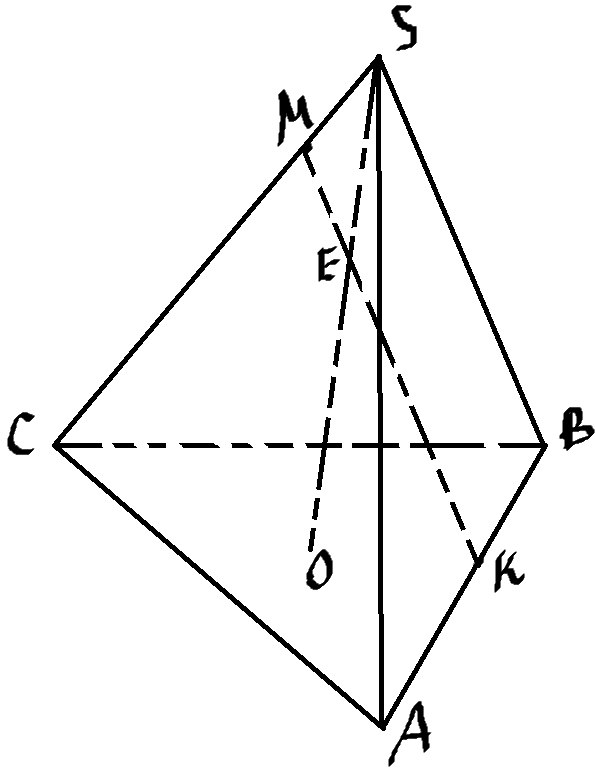
Итак, наша задача найти расстояние между скрещивающимися прямыми \( AC \) и \( MK \)
Чтобы найти это расстояние, мы проведем через точки \( M \) и \( K \) плоскость параллельную прямой \( AC \)
Это сделать очень легко, проведем из точки \( K \) прямую \( KK1 \) параллельную \( AC \)
И прямую \( MM1 \) параллельную \( AC \)
Таким образом, получили плоскость \( MM1KK1 \) параллельную \( AC \)
Сделаем доп построение, построим апофему \( SP \) и соединим \( PB \) (см рисунок)
Плоскость \( PSB \) \( ⊥ \) прямой \( AC \) (так как прямые PS и BP ⊥ AC, PS и PB-высоты)
А прямая \( AC \) параллельная нашей плоскости где содержится \( MK \)
Искомое расстояние \( PH \) (Точки F и V – точки пересечения плоскостей MM1KK1 и SPB)
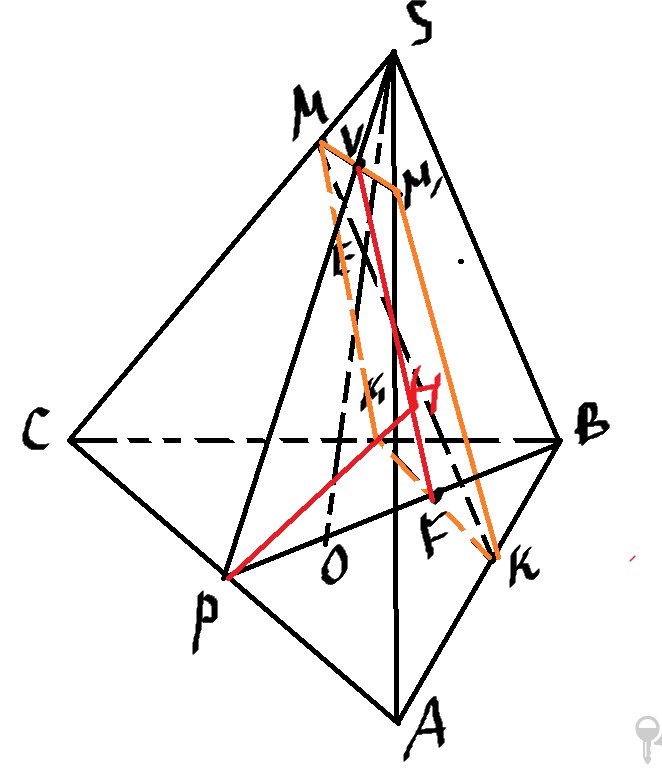
Получился громоздкий рисунок ( у меня он еще и неровный, VF проходит через точку E)
Чтобы найти искомое расстояние, сделаем выносной чертеж на плоскость SPB
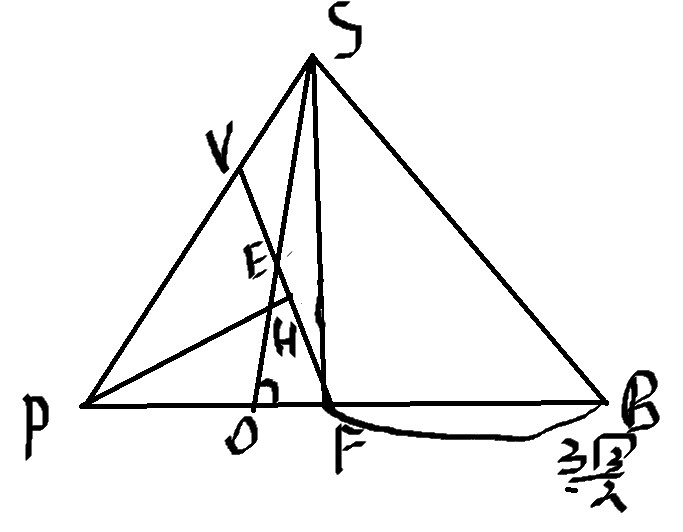
По условие нам известно, что все стороны основание 6, а ребра 4.
Найдем из треугольника \( PBA \) \( PB=\sqrt{AB^2-PA^2}=\sqrt{6^2-3^2}=3\sqrt{3} \)
\( PO+OB=PB \) а в свою очередь по свойству медиан \( \frac{PO}{OB}=\frac{1}{2} \), значит
\( OB=2PO \) получаем, что \( PO=\sqrt{3} \) и \( OB=2\sqrt{3} \)
Заметим, что \( F \) – середина PB, почему? Это можно доказать по теореме Фалеса, или через подобие треугольников, сделайте это самостоятельно:) (вспомните начало построение плоскости MM1KK1, а именно параллельность)
В пункте А мы выяснили, что \( SE=OE \), найдем \( SO=\sqrt{SB^2-OB^2}=\sqrt{16-4*3}=2 \)
\( OF=OB-FB=2\sqrt{3}-\frac{3\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \)
Искомое расстояние можно найти по разному, я допустим найду синус угла \( ∡EFP \) и найду искомое расстояние PH
Из треугольника \( OEF \) \( EF=\sqrt{EO^2+OF^2}=\frac{\sqrt{7}}{2} \)найдем
\( sin∡EFO=\frac{EO}{DF}=\frac{2}{\sqrt{7}} \)
\( sin∡EFO=\frac{PH}{PH} \)
\( PH=sin∡EFO*PF=\frac{2}{\sqrt{7}}*\frac{3\sqrt{3}}{2}=\frac{3\sqrt{21}}{7} \)
Вот и ответик:)
Ответ: \( \frac{3\sqrt{21}}{7} \)
