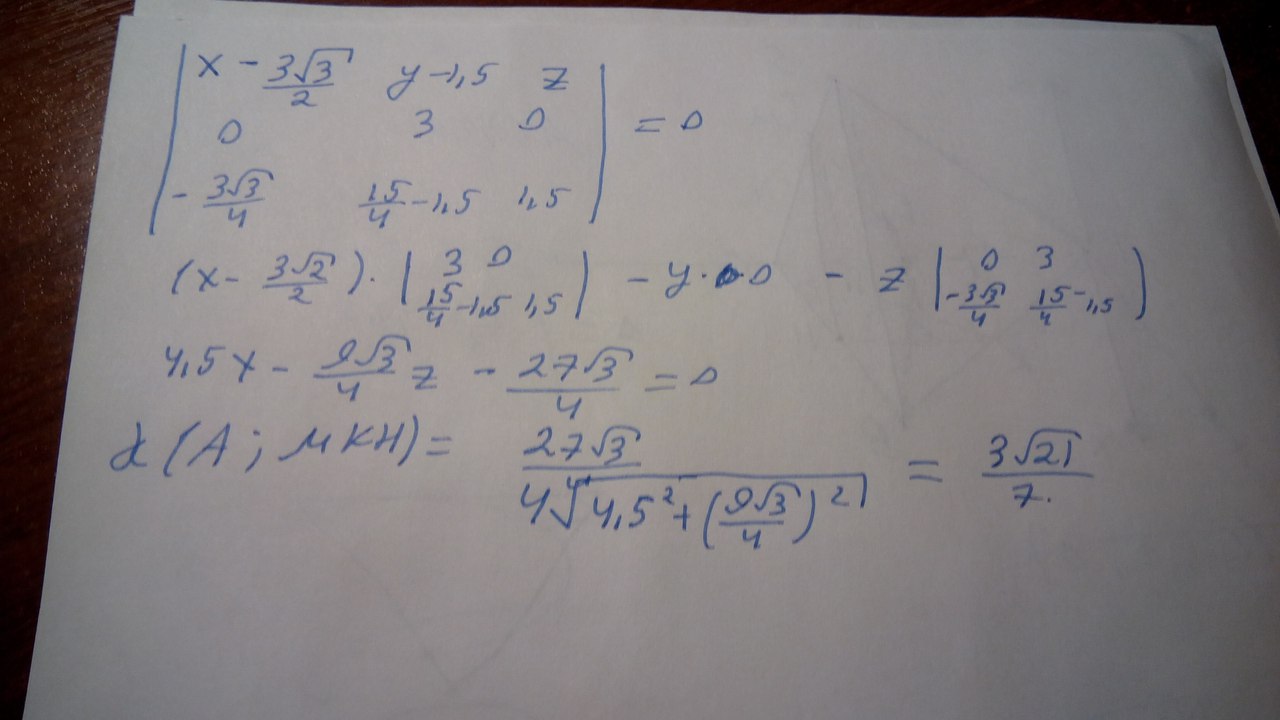14. В правильной треугольной пирамиде SABC точка К – середина ребра АВ. На ребре SC взята точка М так, что SM : СМ = 1:3.
а) Докажите, что прямая МК пересекает высоту SО пирамиды в её середине.
б) Найдите расстояние между прямыми МК и АС, если известно, что АВ=6, SA=4.
Решение
Пункт А
Сделаем рисунок

Сразу напрашивается теорема Менелая!
\( \frac{CM}{SM}*\frac{SE}{EO}*\frac{OK}{KC}=1 \)
Итак, отношение CM к SM мы знаем.
O-точка пересечения медиан, биссектрис и высот. А в точке пересечения медиан, точка O делит KC в отношении 2:1 считая от вершины C, значит \( \frac{OC}{OK}=\frac{2}{1} \)
KC-три части, OK – одна часть
\( \frac{SE}{OE}*3*\frac{1}{3}=1 \) значит
\( \frac{SE}{OE}=1 \) отсюда
\( SE=OE \) – что и требовалось доказать:)
Пункт Б
Я решил сделать два способа решения
Второй способ смотрите по ссылке gdz-larin.ru/?p=807
Решим векторным способом, введем прямоугольную систему координат.
Итак, нужно найти расстояние между скрещивающимися прямыми, проведем плоскость, которая будет параллельна прямой AC и в ней будет содержаться прямая MK (см рисунок)
Введем прямоугольную систему координат, точка А-начало.
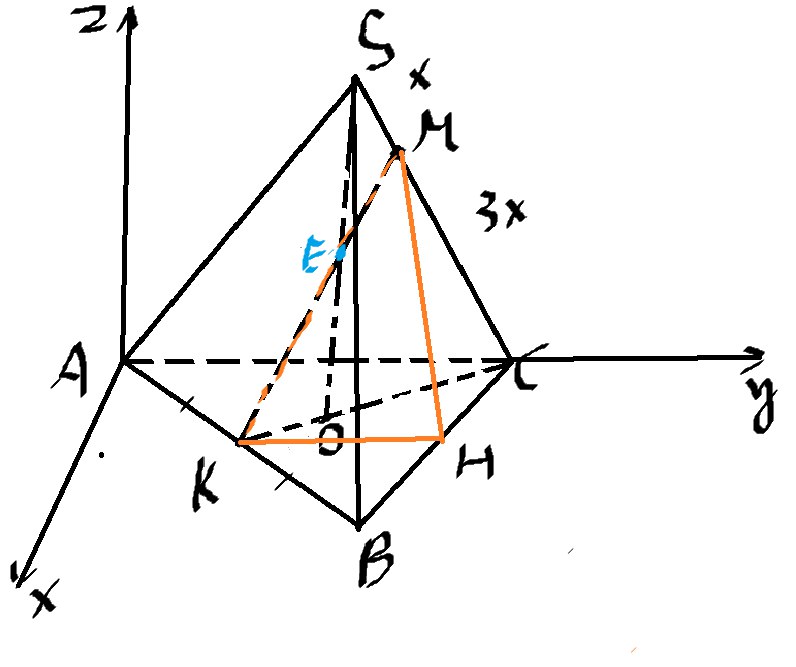
Задача теперь следующая, найти расстояние от точки A или C (я выберу точку А) до плоскости \( MKH \)
Находим координаты точек, сделаем выносной чертеж на плоскость основания.
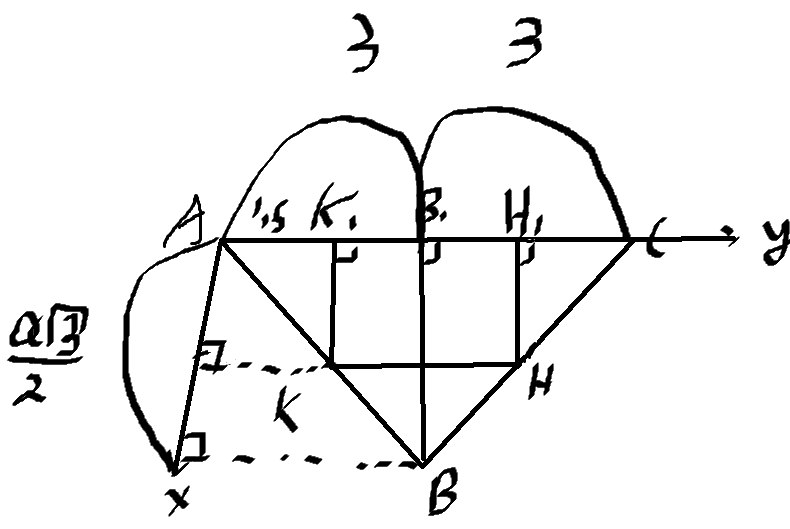
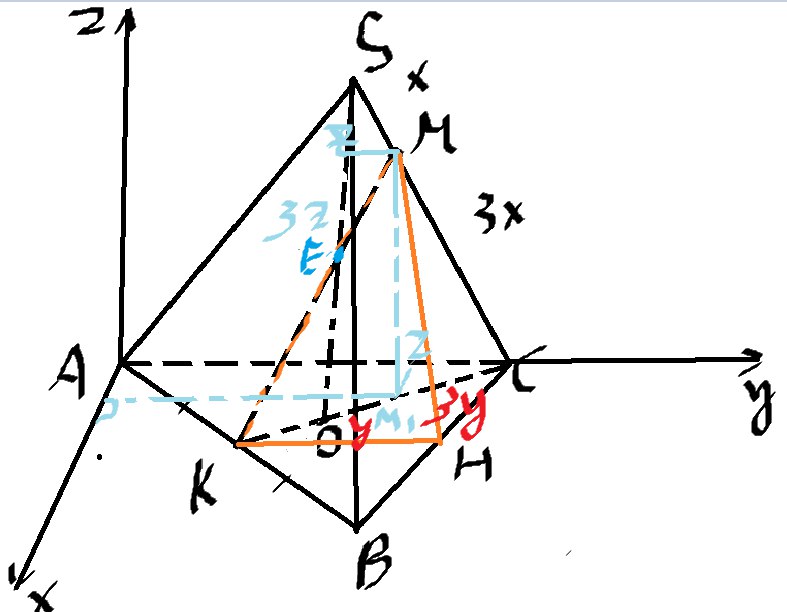
1) Координаты точки \( K(\frac{3\sqrt{3}}{2};1.5;0) \) (так как KK1- средняя линия в треугольнике ABB1) (для нахождения координат опускаем высоты на оси).
2) Координаты точки \( H(\frac{3\sqrt{3}}{2};4.5;0) \)
3) Координаты точки \( M(\frac{3\sqrt{3}}{4};\frac{15}{4};1.5) \) (опять же опускаем высоты на оси, и находим радиус векторы, координаты) (высота пирамиды \( SO=2 \) по т пифагора)
Составим уравнение плоскости, заранее поделив все на d и найдем искомое расстояние (чтобы увеличить кликните по фотографии)

И второй вариант решения через определитель