14. В правильной пирамиде на ребрах АВ и РD взяты точки М и К
соответственно, причем АМ:ВМ = 1:3, DK:РК = 4:3.
PABCD
А) Докажите, что прямая ВР параллельна плоскости МСК.
Б) Найдите площадь сечения пирамиды плоскостью МСК, если известно, что все ребра
пирамиды равны 4.
Решение
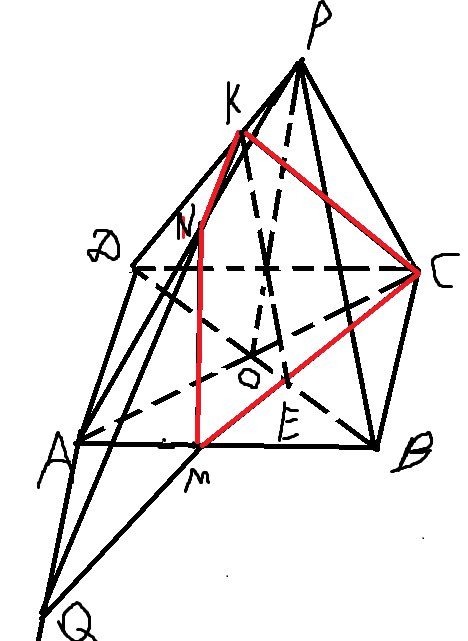
Изобразим пирамиду

Построим сечение:
- Соединим MС и КC, т.к лежат в одной плоскости.
- Продолжим сторону AD до пересечения с прямой MC (Q-точка пересечения)
- Соединим KQ и она пересекает ребро AP в точке N
- Соединяем NM
- Искомое сечение NMKC (чтобы увеличить кликните по фотографии
Пункт А
Пусть E-точка пересечения плоскости MCK и DPB
Обозначим сторону основания за x
\( MB=\frac{3x}{4} \) \( DC=x \)
Треугольник \( MBO \)подобен \( DOC \)(по двум углам)
Запишем отношение сходственных сторон
\( \frac{DC}{MB}=\frac{DE}{EB}=\frac{CE}{ME}=\frac{4}{3} \)
Отсюда главное что \( \frac{DE}{EB}=\frac{4}{3} \)
По обратной теореме Фалеса, прямые KE и BP параллельны
А если BP параллельна прямой KE, которая лежит в плоскости нашего сечения, что BP параллельная плоскости MCK. Вот и все.
Пункт Б (прошу дотерпеть до конца, задача требует внимания) (если хотите более простое решение, то пишите в комменты)
Куча писанины, но если пытаться вникнуть, поверьте, не сложная задача.
Итак, начнем:)
Площадь нашего сечение (выделено красным цветом) Найдем как
\( S=S_{KNME}+S_{KLC} \)
Ясно, что KLC-треугольник, а KNME-трапеция, почему? А мы это сейчас докажем.
BP параллельна плоскости нашего сечения, значит BP параллельна NM и KE, отсюда и NM параллельна KE (так как, если две прямые параллельны третьей прямой, то они между собой параллельны)
Идем дальше
1) Из треугольника \( CMB \) найдем \( CM=\sqrt{MB^2+CB^2}=\sqrt{3^2+4^2}=5 \)
Мы уже в пункте А находили отношение ME к EC. Соответственно найдем эти стороны
\( CM=ME+EC \) , а так как \( \frac{EC}{ME}=\frac{4}{3} \) выражаем \( ME=\frac{3CE}{4} \)
Значит \( 5=\frac{7EC}{4} \) откуда \( EC=\frac{20}{7} \) и \( ME=\frac{15}{7} \)
2) Треугольник \( BPA \) подобен \( ANM \) (по двум углам), запишем подобие
\( \frac{NM}{BP}=\frac{AM}{AB}=\frac{AN}{AP}=\frac{1}{4} \) откуда \( NM=\frac{BP}{4}=1 \)
3) Делаем дополнительное построение, опустим высоту KH1 на BD и высоту KH2 на CM. Потом поймете зачем. (должно получится так)
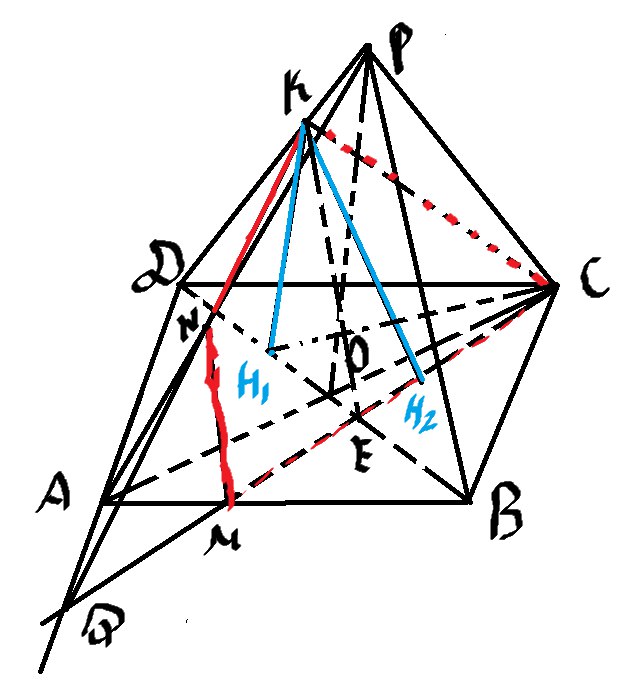
По теореме о 3-х перпендикулярах H1H2 ⊥ СM и KH1 ⊥ BD (KH1-перпендикуляр, KH2-наклонная, H1H2-проекция)
4) Уже можно догадаться что мы будем делать. KH2-высота в треугольнике \( KEC \), площадь которого нам нужно найти. Вот высоту мы и будем искать, так как основание EC мы уже знаем.
Найдем сначала площадь треугольника \( ECH1 \) и выразим H1H2
\( S=0.5*CE*H1H2=0.5H1E*CO \) (СO⊥BD) выражаем \( H1H2=\frac{H1E*CO}{EC} \)
\( BD=4\sqrt{2} \) – как диагональ квадрата (по т. Пифагора)
5) В пункте А находили подобие треугольников \( MEB \) и \( CED \), запишем отношение
\( \frac{BE}{DE}=\frac{3}{4} \) выразим \( DE=\frac{16\sqrt{2}}{7} \)
Можно увидеть, что треугольник \( DKE \) – равнобедренный (\( DK=KE \))
KH1-это высота и медиана. (по свойству равнобедренного треугольника)
Значит \( H1E=0.5DE=\frac{8\sqrt{2}}{7} \), а \( CO=0.5BD \)
Найдем \( H1H2=\frac{H1E*CO}{EC}=\frac{32}{20}=\frac{8}{5} \)
6) Из треугольника \( KDH1 \) найдем \( KH1=\sqrt{KD^2+H1D^2}=\sqrt{(\frac{16}{7})^2-(\frac{8\sqrt{2}}{7})^2}=\frac{8\sqrt{2}}{7} \)
7) Найдем \( KH2=\sqrt{KH1^2+H1H2^2}=\sqrt{(\frac{8}{5})^2+(\frac{8\sqrt{2}}{7})}=\frac{24\sqrt{11}}{35} \)
\( S_{KEC}=0.5*CE*KH2=0.5*\frac{20}{7}*\frac{24\sqrt{11}}{35}=\frac{48\sqrt{11}}{49} \)
Вот мы и нашли одну из площадей)
8) Надеюсь, ты еще здесь:) Идем дальше!
Треугольник \( AQM \) подобен \( CMB \) (по двум углам), запишем подобие
\( \frac{AM}{MB}=\frac{QM}{CM}=\frac{1}{3} \), отсюда \( QM=\frac{1}{3}CM=\frac{5}{3} \)
\( QE=QM+ME=\frac{5}{3}+\frac{15}{7}=\frac{80}{21} \)
9) А треугольник \( QNM \) подобен \( QKE \)
\( \frac{QM}{QE}=\frac{NM}{KE}=\frac{7}{16} \), а площади относятся как квадрат подобия этих треугольников
\( \frac{S_{QNM}}{S_{QKE}}=k^2=\frac{49}{256} \)
А в свою очередь \( S_{KNME}=S_{QKE}-S_{QNM}=S_{QKE}-\frac{49}{256}S_{QKE}=S_{QKE}(1-\frac{49}{256}) \)
Найдем площадь треугольника \( S_{QKE}=0.5*QE*KH2=0.5*\frac{80}{21}*\frac{24\sqrt{11}}{35} \)
Соответственно найдем \( S_{KNME}=\frac{207\sqrt{11}}{196} \)
10) Теперь же пора найти площадь нашего сечения))
\( S=S_{KEC}+S_{KNME}=\frac{57\sqrt{11}}{28} \)
Ответ: \( \frac{57\sqrt{11}}{28} \)
