14. В прямоугольном параллелепипеде ABCDA1B1C1D1 а ребре С1D1 взята
очка К так, что КС1=3КD1
А) Докажите, что плоскость АСК делит диаго и 4:1, считая от точки В.
Б) Найдите расстояние от точки D до пл естно, что АВ=4, ВС=3,
СС1=2.
Решение
Главное в 14 номере – это правильный рисунок.
Построим сечение
Так как точки K и C лежат в одной плоскости их можно соединить. Плоскость сечения пересекает две параллельные плоскости (нижнюю и верхнюю), значит линии их пересечения параллельны. Построим прямую NK параллельную AC. Прямая NK пересекет ребро A1D1 в точке N.
Точка N лежит в одной плоскости с A соединяем. Получаем искомое сечение ACNK
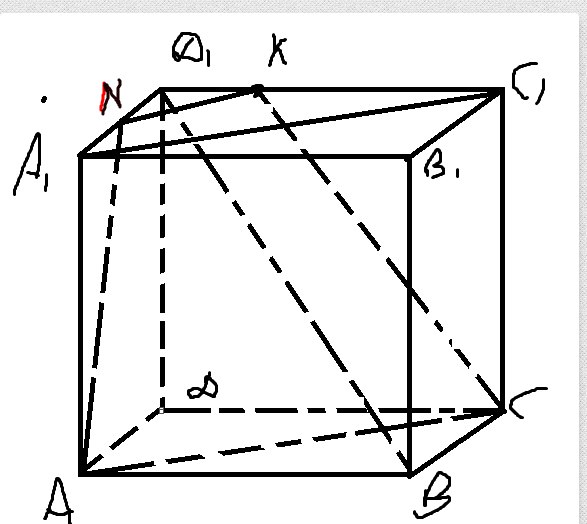
Это сечение пересекает диагональ D1B в какой-то точке. Прямая D1B содержится в плоскости DBB1D1. Проведем прямые DB и D1B1 и соединим точки пересечения. (O2 и O1 – точки пересечения плоскостей ACK и DBB1D1)
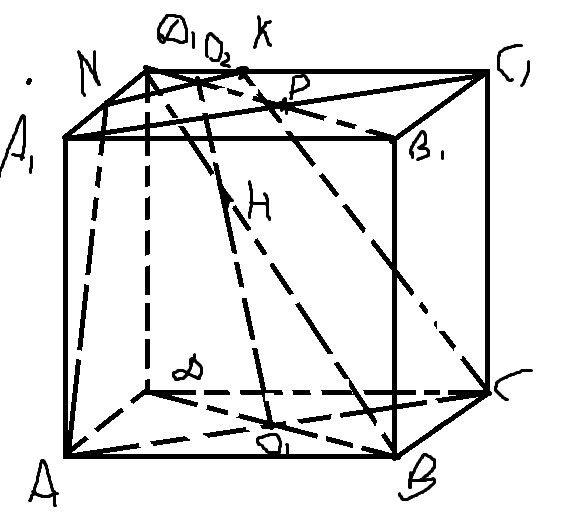
Итак, нужно доказать что точка H делит диагональ BD1 в отношении 4:1 считая от B.
Докажем.
Треугольники \( D1HO2 \) и \( HO1B \) подобны по двум углам.
Запишем отношение сходственных сторон \( \frac{D1H}{HB}=\frac{D1O2}{O1B}=\frac{O2H}{HO1} \)
Треугольники \( ND1K \) и \( A1D1C1 \) подобны по двум углам. И их коэффициент подобия равен 1/4
\( \frac{D1O2}{D1P}=\frac{D1K}{D1C1}=\frac{1}{4} \)
А так как \( O1B=D1P \), то
\( \frac{D1H}{HB}=\frac{D1O2}{D1P}=\frac{1}{4} \) что и требовалось доказать.
Теперь же пункт б
Сразу же напрашивается векторный способ
Введем прямоугольную систему координат, пусть точка B(0;0;0)
Дальнейшее решение на листочке. (чтобы увеличить, кликните по фотке)

