14. Внутри куба расположены два равных шара, касающихся друга. При этом один
шар касается трех граней куба, имеющих общую вершину, а другой касается трех
оставшихся граней.
а) Докажите, что центры шаров принадлежат диагонали куба, исходящей из общей
для граней вершины.
б) Найдите радиусы этих шаров, если ребро куба равно 13.
Решение:
Пункт а
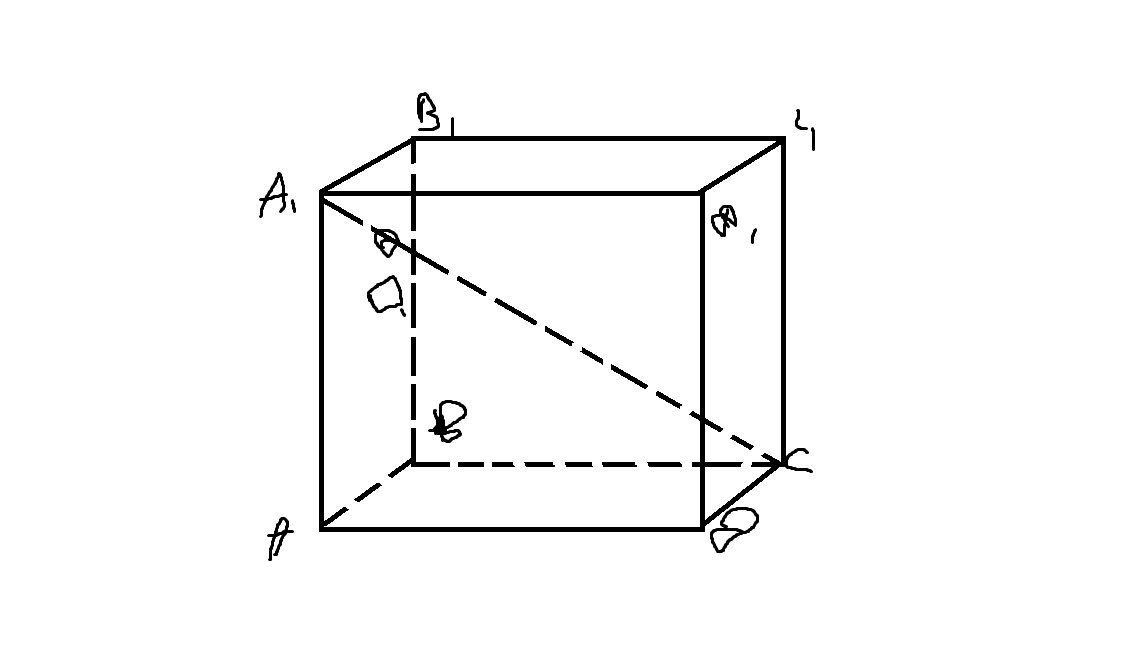
Будем доказывать коллинеарность векторов (то есть, что они лежат на одной прямой или на параллельных прямых)
Введем прямоугольную систему координат. Пусть центр первого шара буква O1. Расположен где-то на прямой A1C
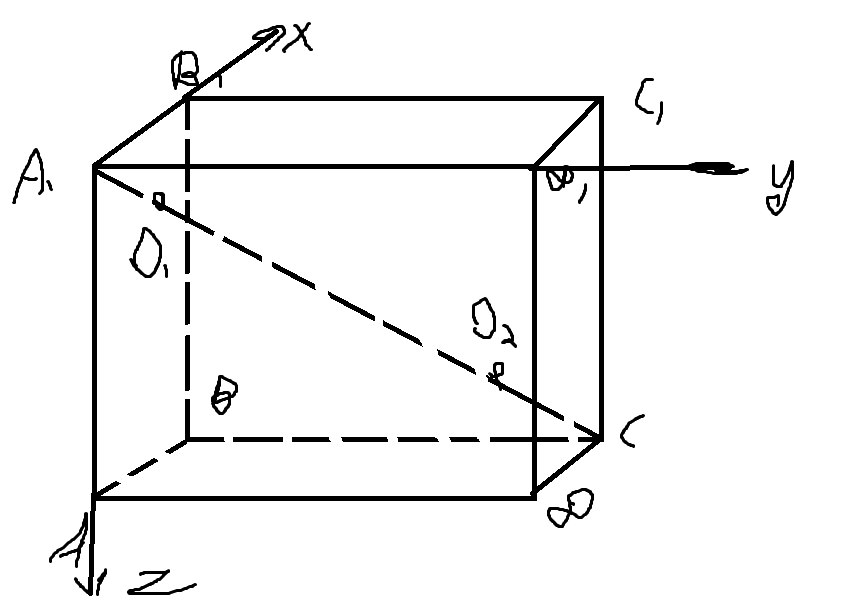
Пусть ребро куба x а радиусы шаров R
Координаты точки A1(0;0;0) координаты C(x;x;x) координаты O1(R;R;R) (так как точка O1 равноудалена от граней)
Координаты вектора A1C{x;x;x} (из координаты конца вычитаем координаты начала)
Координаты вектора A1O1{R;R;R}
Если координаты векторов пропорциональны друг другу, то они коллинеарны.
Мы видим что координаты двух векторов A1C и A1O1 пропорциональны друг другу, то есть они лежат на одной прямой, что и требовалось доказать.
Для центра другого шара доказывается аналогично, при этом можно ввести другую систему координат с центром в C1
Пункт б
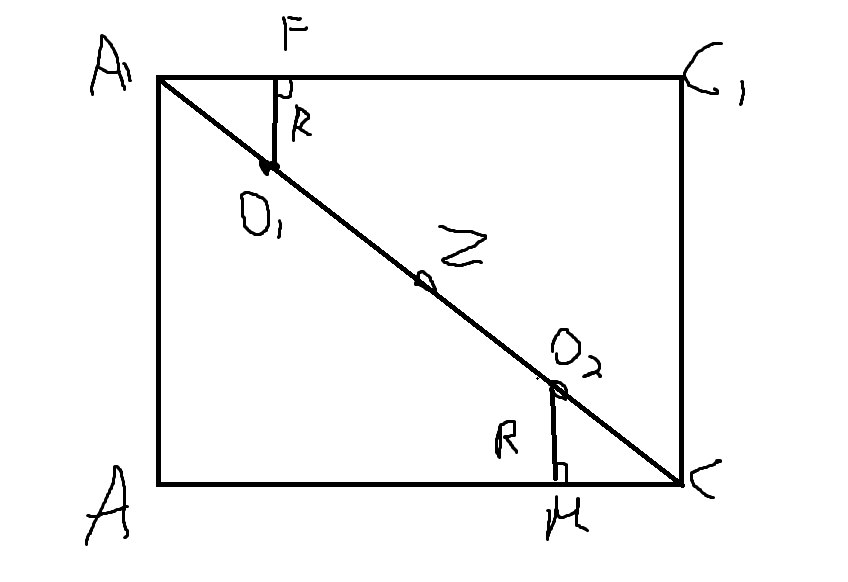
Сделаем выносной чертеж на диагональное сечение куба AA1C
В нем O1 и O2 центры шаров, Z-точка пересечения шаров, O1F и O2M – радиусы.
При этом \( O1Z=ZO2=R \) так как это радиусы проведенные в точку касания.
Диагональ куба равна \( A1C^2=x^2+x^2+x^2 \) \( A1C=x\sqrt{3} \)
\( A1C=A1O1+O1Z+ZO2+O2C=2A1O1+2R \)
Треугольники \( A1O1F \) и \( O2MC \) равны по острому углу и катету
Выразим синус угла ACA1 из прямоугольного треугольника ACA1 он будет равен \( sina=\frac{1}{\sqrt{3}} \)
Так как углы CA1C1 и ACA1 равны как накрест лежащие, то найдем сторону A1O1 и подставим в уравнение выше.
\( A1O1= \frac{FO1}{sina}=\sqrt{3}R \)
При этом A1C как мы выяснили равен \( A1C=x\sqrt{3} \)
\( x\sqrt{3}=2R+2R\sqrt{3} \)
Отсюда выражаем R и получаем
\( R=\frac{x\sqrt{3}}{2(\sqrt{3}+1)}=\frac{13\sqrt{3}}{2(\sqrt{3}+1)} \)
