14. На диагонали АВ1 грани АВВ1А1 треугольной призмы взята точка М так, что
АМ : МВ1 = 5 : 4.
а) Постройте сечение призмы плоскостью, проходящей через точку М, параллельно
диагоналям А1С и ВС1 двух других граней.
б) Найдите в каком отношении плоскость сечения делит ребро СС1
Решение:
Решил расписать все как можно подробнее. Если есть вопросы, то обязательно задавайте, я всегда отвечу.
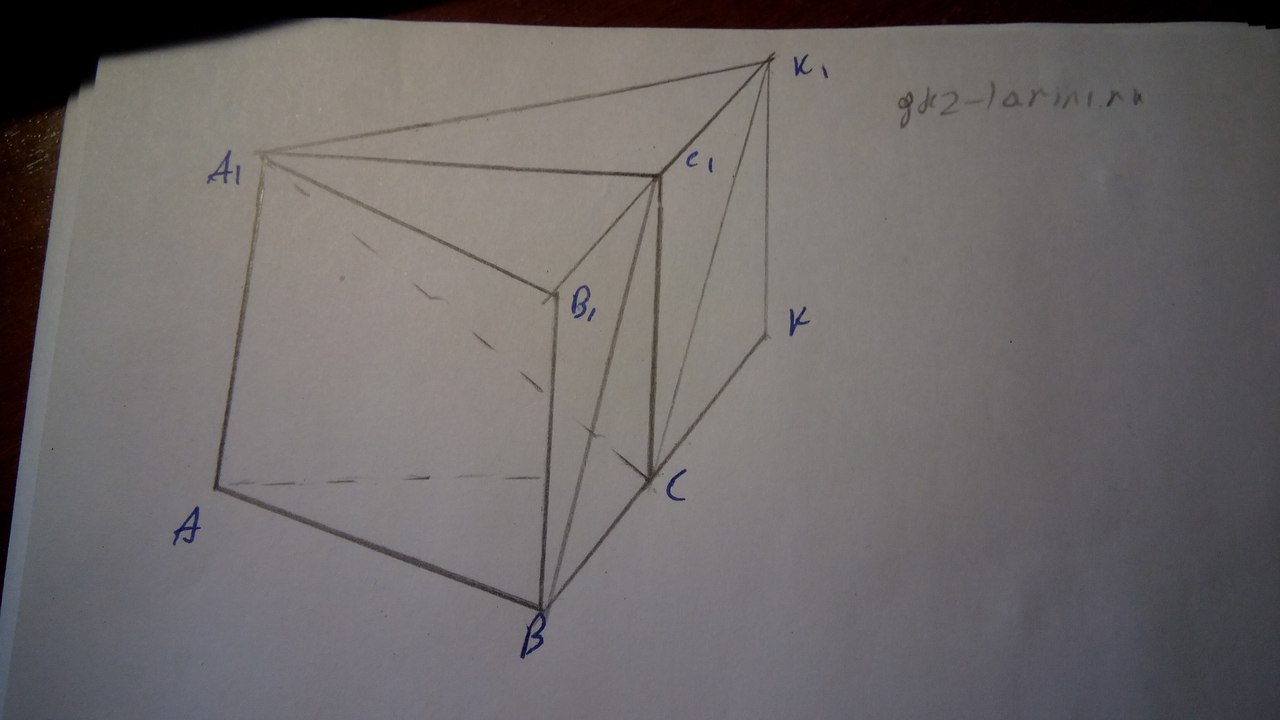
Заметим, что прямые A1C и BC1 являются скрещивающимися. Построим плоскость, которая будет параллельная прямой BC1. На продолжении BC отложим CK=BC и C1K=B1C1. При этом его диагональ CK1=BC1. Прямые CK1 и A1C пересекаются в точке C и значит определяют плоскость \( A1CK1 \).
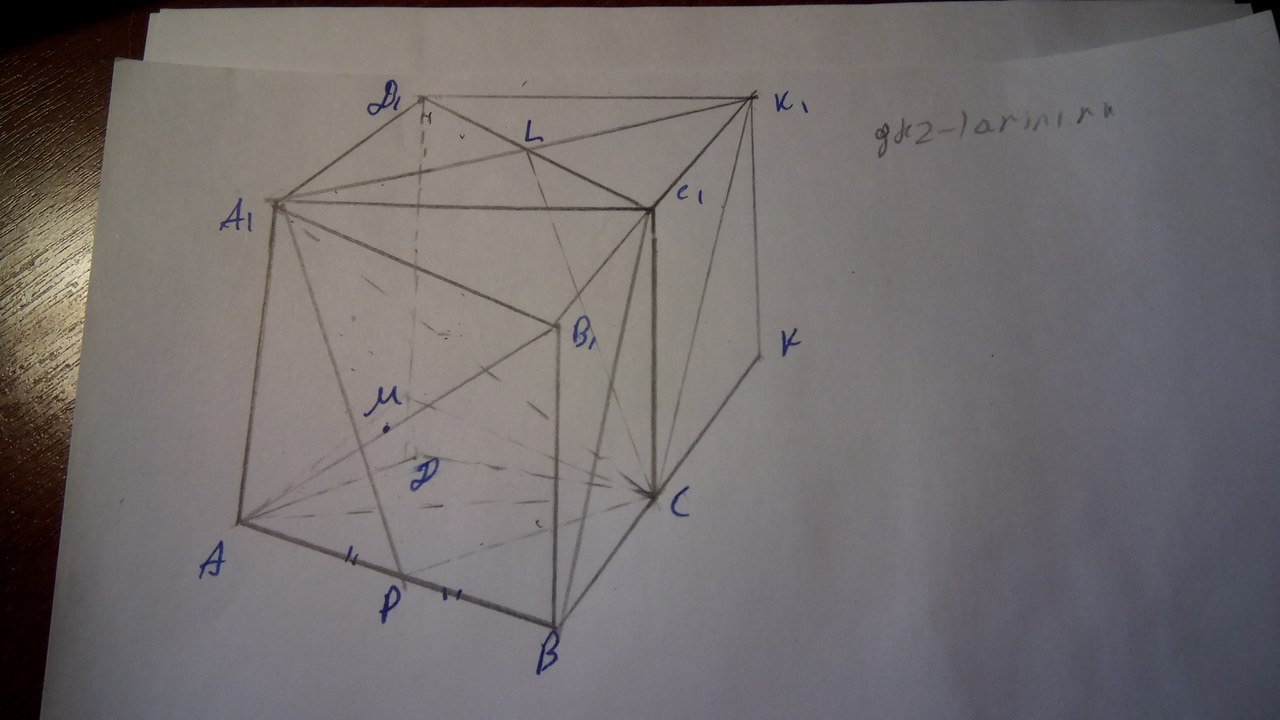
Достроим нашу треугольную призму до четырехугольной. Проведем прямую CL, где L точка пересечения диагоналей паралеллограмма \( A1D1K1C1 \) не трудно догадаться, что она будет серединой по свойству диагоналей. Построим сечением плоскости \( A1K1C \) и плоскостью четырехугольной призмы.

Построим PC параллельную LA1, при этом P середина AB. Соединим точки P и A1 и получаем сечение плоскости A1K1C с призмой, сечение – A1LCP
Теперь строим искомое сечение через M параллельную нашему сечению, которые мы построили. Строим из точки M прямую параллельную A1P (F-точка пересечения с ребром A1B1, точка N-точка пересечения с AB). Из точки F строим прямую параллельную AL (E-точка пересечения с ребром A1C1) Через N проводим прямую параллельную PC (Т-след секущей плоскости на ребре BC). Из точки T проводим прямую параллельную BC, получаем точку X, и так как точки E и X лежат в одной плоскости, то их соединяем. Получаем сечение \( FEXNT \)
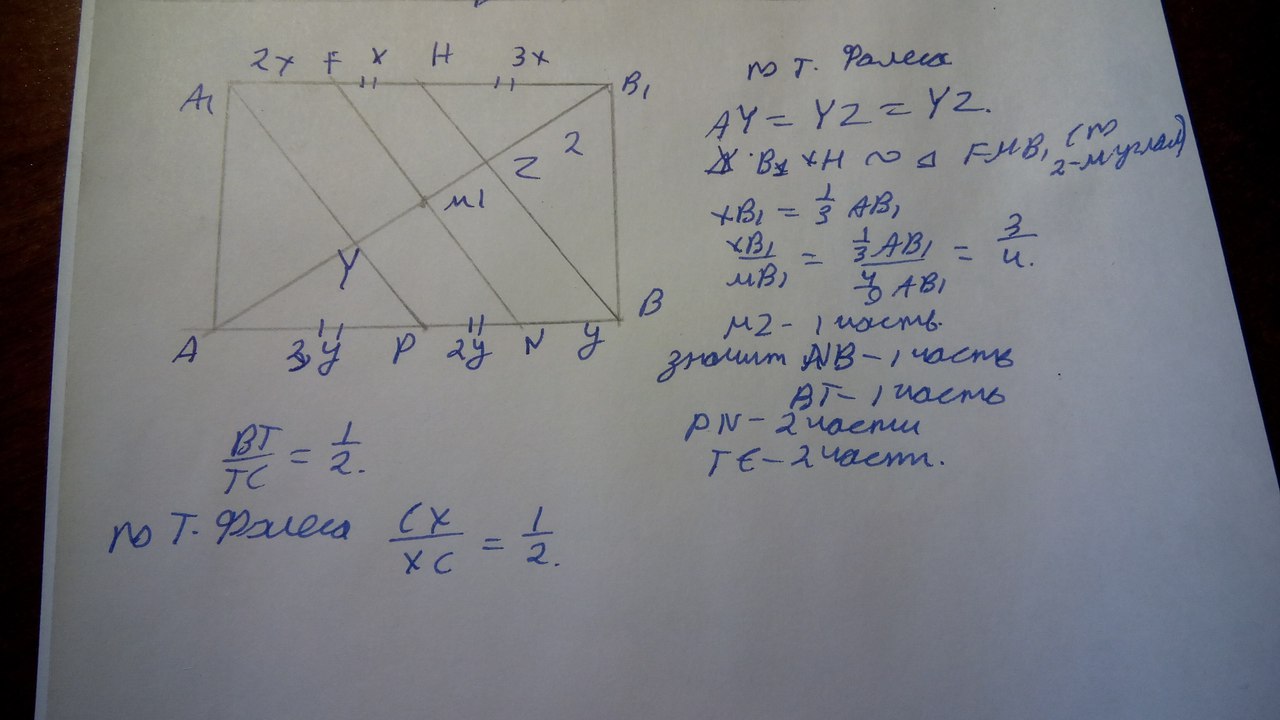
Теперь ответим на пункт Б
Найдем отношение C1X к XC
Сделаем выносной чертеж грани \( A1ABB1 \) и проведем BH (H-середина A1B1)
Дальнейшее решение показано на листочке.