А) Решите уравнение
\( cos^6x+sin^6x=\frac{1}{4}sin^22x \)
Б) Найдите все корни уравнения, принадлежащие промежутку (\( \frac{3\pi}{4};\frac{\pi}{2} \)]
Решение
\( a^3+b^3=(a+b)(a^2-ab+b^2) \)
\( (cos^2x)^3+(sin^2x)^3= \)
\( =(sin^2x+cos^2x)(sin^4x-sin^2*cos^2x+cos^4x)= \)
\( =sin^4x-sin^2x*cos^2x+cos^4x= \)
\( =(sin^2x+cos^2x)^2-3sin^2x*cos^2x=1-3*sin^2x*cos^2x=1-\frac{3}{4}sin^22x \)
\( 1-\frac{3}{4}sin^22x=\frac{1}{4}sin^22x \)
\( sin^22x=1 \)
\( sin2x=1 \)
\( sin2x=-1 \)
\( x=\frac{\pi}{4}+\pi n \)
\( x=±\frac{3\pi}{4}+\pi n \)
\( x=±\frac{\pi}{4}+\pi n \)
Объединяя корни
\( x=\frac{\pi}{4}+\frac{\pi n}{2} \)
Б) Легко отобрать на тригонометрической окружности
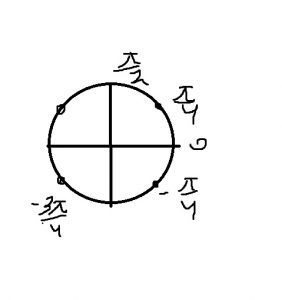
\( x=±\frac{\pi}{4} \)
а) \( x=\frac{\pi}{4}+\frac{\pi n}{2} \) б) \( x=±\frac{\pi}{4} \)
