а) Решите уравнение \( (cosx-sinx)^2+\sqrt{2}sin(\frac{3\pi}{4}-2x)+\sqrt{3}cosx=0 \)
б) укажите корни этого уравнения, принадлежащие отрезку [\( -\frac{4\pi}{3};-\frac{2\pi}{3} \)]
Решение
\( (cosx-sinx)^2=cos^2x-2sinxcosx+sin^2x=1-sin2x \)
\( \sqrt{2}sin(\frac{3\pi}{4}-2x)=cos2x+sin2x \)
\( 1-sin2x+cos2x+sin2x+\sqrt{3}cosx=cos2x+\sqrt{3}cosx+1 \)
\( 2cos^2x+\sqrt{3}cosx=0 \)
\( cosx(2cosx+\sqrt{3})=0 \)
\( cosx=0 \)
\( cosx=-\frac{\sqrt{3}}{2} \)
\( x=\frac{\pi}{2}+\pi n \)
\( x=±\frac{5\pi}{6}+2 \pi n \)
Б) легко отобрать на тригонометрической окружности
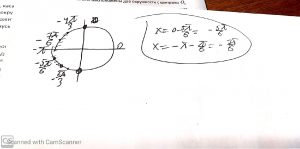
Ответ: а) \( x=\frac{\pi}{2}+\pi n \),\( x=±\frac{5\pi}{6}+2 \pi n \)б) \( x=-\frac{7\pi}{6},-\frac{5\pi}{6} \)
