а) Решите уравнение \( \frac{16^{sinx}-3*4^{0.5+sinx}+8}{log_{2}(1-3cosx)}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [\( -\frac{3\pi}{4};\frac{6\pi}{5} \)]
Решение
ОДЗ
\( 1-3cosx>0 \), значит \( cosx<\frac{1}{3} \)
\( 1-3cosx\neq1 \), значит \( cosx \neq 0 \)
Теперь поработаем числителем
Сделаем очевидную замену на \( 4^{sinx}=t,t>0 \)
\( t^2-6t+8=0 \)
\( t=4 \)
\( t=2 \)
\( 4^{sinx}=4 \), откуда \( sinx=1 \)
\( 4^{sinx}=2 \), откуда \( sinx=0.5 \)
Но не забываем про ОДЗ \( cosx \neq 0 \) , значит \( x\neq \frac{\pi}{2}+\pi n \), \( sinx=1 \) – нам не подходит
Теперь с \( cosx<\frac{1}{3} \)
Для удобства изобразим рисунок
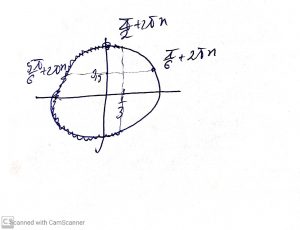
Видим, что еще один корень “отлетает”
Значит ответ на пункт а запишем так:
\( x=\frac{5 \pi}{6}+2 \pi n \)
Б) Легко отобрать корни на той же окружности:)
Я лишь запишу ответ
\( x=\frac{5 \pi}{6} \)
Ответ: а) \( x=\frac{5 \pi}{6}+2 \pi n \)б) \( x=\frac{5 \pi}{6} \)
