а) Решите уравнение \( 2sin^2x+sinx*cosx+\sqrt{3}(sin2x+cos^2x)=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [\( \frac{5\pi}{6};\frac{11\pi}{6} \)]
Решение
Это стандартное однородное уравнение. Мы его решаем так:
Делим все уравнение на \( cos^2x \neq0 \)
\( 2tg^2x+(2\sqrt{3}+1)tgx+\sqrt{3}=0 \). Делая замену \( tgx=t \) решаем квадратное уравнение
\( tgx=-\sqrt{3} \)
\( tgx=-0.5 \)
\( x=-\frac{\pi}{3}+\pi n \)
\( x=-arctan(0.5)+\pi n \)
Б) Легко можно отобрать на тригонометрической окружности
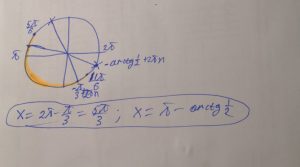
Ответ: а) \( x=-\frac{\pi}{3}+\pi n \),\( x=-arctan(0.5)+\pi n \)б) \( x=\pi-arctg0.5,\frac{5\pi}{3} \)
