а) Решите уравнение
\( sin^2(x+\frac{\pi}{4})=sin^2(\frac{\pi}{4}-x)+\sqrt{7}cosx \)
Решение
\( (\frac{1}{\sqrt{2}}cosx+\frac{1}{\sqrt{2}}sinx)^2=(\frac{1}{\sqrt{2}}cosx-\frac{1}{\sqrt{2}}sinx)^2+\sqrt{7}cosx \)
\( 0.5(1+2sinx*cosx)=0.5(1-2sinx*cosx)+\sqrt{7}cosx \)
\( cosx(2sinx-\sqrt{7})=0 \)
\( cosx=0 \)
\( sinx=\frac{\sqrt{7}}{2}>1 \) – нет решений
\( x=\frac{\pi}{2}+\pi n \)
Б)
Легко отобрать корни на окружности
\( e≈2,71 \) радиан
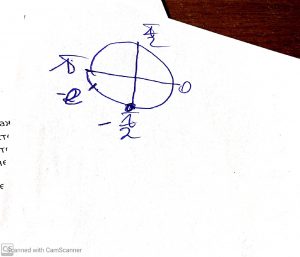
Ответ: а) \( x=\frac{\pi}{2}+\pi n \) б) \( x=-\frac{\pi}{2},\frac{\pi}{2} \)
