а) Решите уравнение
\( \sqrt{2}cos(x+\frac{\pi}{4})-sinx=|cosx| \)
б) Найдите все корни уравнения, принадлежащие отрезку [\( 19 \pi;\frac{41}{2}\pi \)]
Решение
\( cos(x+\frac{\pi}{4})=\frac{1}{\sqrt{2}}(cosx-sinx) \)
\( cosx-2sinx=|cosx| \)
Рассмотрим два случая
1. \( cos>=0 \)
\( cosx-2sinx=cosx \)
\( sinx=0 \)
\( x=\pi n \), но т.к \( cosx>=0 \) (1,4 четверть), то \( x=2 \pi n \)
2. \( cosx<0 \) (2,3 четверть)
\( sinx-cosx=0 \)
Стандартный прием домножим все уравнение на \( \frac{\sqrt{2}}{2} \)
\( sinx*cos\frac{\pi}{4}-cosx*sin\frac{\pi}{4}=0 \)
\( sin(x-\frac{\pi}{4})=0 \)
\( x=\frac{\pi}{4}+\pi n \), но т.к \( cosx<0 \), то
\( x=\frac{5 \pi}{4}+2\pi n \)
Б) Легко отобрать на тригонометрической окружности
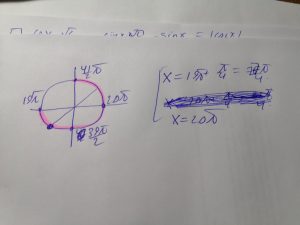
Ответ: а) \( x=2\pi n \), \( x=\frac{5\pi }{4}+2\pi n \), Б) \( x=\frac{77 \pi}{4},20\pi \)
