А) Решите уравнение \( log_{\sqrt{2}sinx}(1+cosx)=2 \)
Б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{2 \pi}{3};\frac{\pi}{3}] \)
Решение
ОДЗ
\( cosx>-1 \)
\( sinx>0 \), \( \pi +2\pi n <x<2\pi n \)
\( sinx \neq\frac{\sqrt{2}}{2} \), \( x \neq (-1)^n \frac{\pi}{4}+\pi n \)
решаем само уравнение
\( 1+cosx=2sin^2x \)
\( 1+cosx=2-2cos^2x \)
\( 2cos^2x+cosx-1=0 \)
\( cosx=-1 \) – не подходит под ОДЗ
\( cosx=0,5 \)
\( x=±\frac{\pi}{3}+2\pi n \), но тут т.к \( sinx>0 \) (1,2 четверть) , но одна серия корней “отлетает”
\( x=\frac{\pi}{3}+2\pi n \)
Б) Легко отобрать на тригонометрической окружности
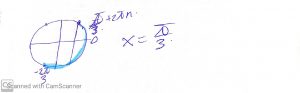
Ответ: а) \( x=\frac{\pi}{3}+2\pi n \), б) \( x=\frac{\pi}{3} \)
