а) Решите уравнение
\( 2021^{sin^4x+cos^4(x-\frac{\pi}{4})}=(2020+(sinx+cosx)^2-sin2x)^\frac{1}{4} \)
б) Укажите корни этого уравнения, принадлежащие отрезку
\( [-\frac{\pi}{log_{2020}4080400};3log_{2021}(2010+lg10^{11})^\pi] \)
Решение
\( 2021^{sin^4x+cos^4(x-\frac{\pi}{4})}=(2020+sin^2x+2sinxcosx+cos^2x-2sinxcosx)^\frac{1}{4} \)
\( 2021^{sin^4x+cos^4(x-\frac{\pi}{4})}=(2021)^\frac{1}{4} \)
\( sin^4x+cos^4(x-\frac{\pi}{4})=1 \)
Воспользуемся формулами понижения степени, кто не помнит, стыдоба.
\( (\frac{1-cos2x}{2})^2+(\frac{1+cos(2x-\frac{\pi}{2})}{2})^2=\frac{1}{4} \)
\( (1-cos2x)^2+(1+sin2x)^2=1 \)
\( sin2x-cos2x+1=0 \)
Тут способов много, но один из моих любимых, да и самых простых – метод вспомогательного угла. Мы его сто раз делали в предыдущих заданиях. Умножаем все уравнение на
\( \frac{1}{\sqrt{2}}=sin\frac{\pi}{4} \) или \( \frac{1}{\sqrt{2}}=cos\frac{\pi}{4} \)
\( cos\frac{\pi}{4}*sin2x-sin\frac{\pi}{4}cos2x=-\frac{1}{\sqrt{2}} \)
\( sin(2x-\frac{\pi}{4})=-\frac{1}{\sqrt{2}} \)
\( 2x-\frac{\pi}{4}=-\frac{\pi}{4}+2 \pi n \)
\( 2x-\frac{\pi}{4}=-\frac{3\pi}{4}+2 \pi n \)
\( x=\pi n \)
\( x=-\frac{\pi}{4}+\pi n \)
Б) Отрезок конечно пугает, но его можно легко упростить \( log_{2020}(4080400)=log_{2020}2020^2=2 \)
\( \pi log_{2021}(2010+11)=\pi \)
Получаем отрезок \( [-\frac{\pi}{2};3\pi] \)
Отбор легко провести на тригонометрической окружности
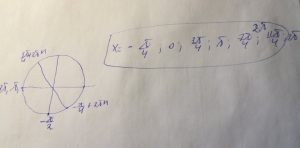
Ответ: а) \( x=\pi n \),\( x=-\frac{\pi}{4}+\pi n \) б) \( x=-\frac{\pi}{4},0,\frac{3\pi}{4},\pi,\frac{7\pi}{4},2\pi,\frac{11\pi}{4},3\pi \)
