а) Решите уравнение \( 16(sin^6x+cos^6x)=13 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [2pi;3pi]
Решение
Легко можно заметить сумму кубов
\( (sin^2x)^3+(cos^2x)^3=\frac{13}{16} \)
\( (sin^2x+cos^2x)(sin^4x-sin^2x*cos^2x+cos^4x)=\frac{13}{16} \)
\( sin^4x-sin^2x*cos^2x+cos^4x=\frac{13}{16} \)
Похоже на сумму квадратов, но не совсем:)
\( sin^4x-sin^2x*cos^2x+cos^4x+2sin^2x*cos^2x-2sin^2x*cos^2x=\frac{13}{16} \)
\( (sin^2x+cos^2x)^2-2sin^2x*cos^2x=\frac{13}{16} \)
\( 1-3*sin^2x*cos^2x=\frac{13}{16} \)
\( 1-\frac{3}{4}sin^22x=\frac{13}{16} \)
\( sin^22x=\frac{1}{4} \)
\( sin2x=±0,5 \)
\( x=±\frac{\pi}{12}+\pi n \)
\( x=±\frac{5\pi}{12}+\pi n \)
или короче \( x=±\frac{\pi}{12}+\frac{\pi n}{2} \)
Б) Легко отобрать корни на тригонометрической окружности (чтобы увеличить кликните по фотке)
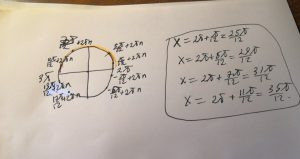
Ответ: а) \( x=±\frac{\pi}{12}+\frac{\pi n}{2} \) б) \( x=\frac{25 \pi}{12},\frac{29 \pi}{12},\frac{31 \pi}{12},\frac{35 \pi}{12} \)
