а) Решите уравнение \( sin3x*cos4x=1 \)
б) Укажите корни этого уравнения, принадлежащие промежутку (-0,5pi;3,5pi]
Решение
Так как \( -1≤sinx≤1 \) и \( -1≤cosx≤1 \)
То, получаем две системы
1) \( sin3x=1 \) и \( cos4x=1 \)
2) \( sin3x=-1 \) и \( cos4x=-1 \)
Разберемся с 1-ой
\( x=\frac{\pi}{6}+\frac{2\pi n}{3} \)
\( x=\frac{\pi}{2}n \)
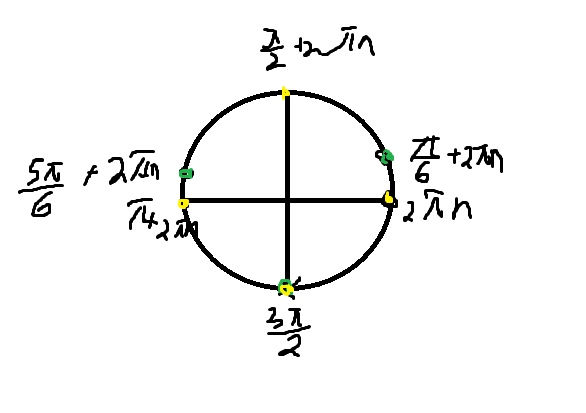
Видим, что совпадение в одной точке \( x=-\frac{\pi}{2}+2\pi n \)
Теперь со 2-ой системы
\( x=-\frac{\pi}{6}+\frac{2\pi n}{3} \)
\( x=\frac{\pi}{4}+\frac{\pi n}{2} \)
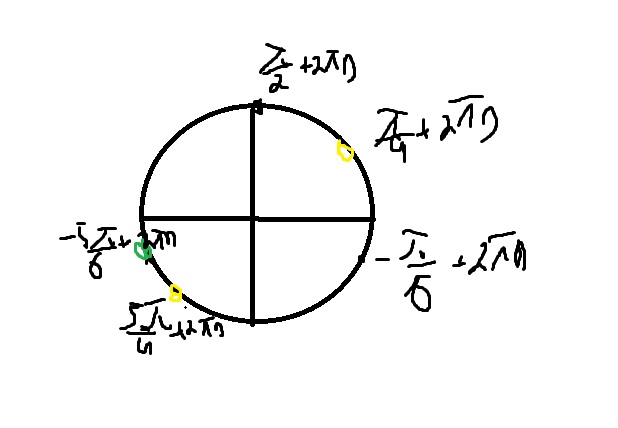
Тут точки нигде не совпали, значит решений нет
Ответ на пункт а)\( x=-\frac{\pi}{2}+2\pi n \)
Б) легче отобрать на окружности (можно использовать тот же рисунок)
Тогда \( x=\frac{3\pi}{2},\frac{7\pi}{2} \)
Ответ: а) \( x=-\frac{\pi}{2}+2\pi n \) б) \( x=\frac{3\pi}{2},\frac{7\pi}{2} \)
