а) Решите уравнение \( cos2x-sin^3x*cosx+1=sin^2x+sinx*cos^3x \)
б) Укажите корни этого уравнения, принадлежащие промежутку (-arctg2;pi)
Решение
\( cos^2x-sin^2x-sin^3x*cosx+1=sin^2x+sinx*cos^3x \)
\( 2cos^2x-1-sin^3x*cosx+1=sin^2x+sinx*cos^3x \)
\( 2cos^2x-sinx*cosx(sin^2x+cos^2x)=sin^2x \)
\( 2cos^2x-sinx*cosx-sin^2x=0 \) Делим все уравнение на \( cos^2x≠0 \)
\( 2-tgx-tg^2x=0 \)
Делаем замену \( tgx=t \) и решаем квадратное уравнение
\( tgx=-2 \)
\( tgx=1 \)
\( x=-acrtg2+\pi n \)
\( x=\frac{\pi}{4}+\pi n \)
Б)
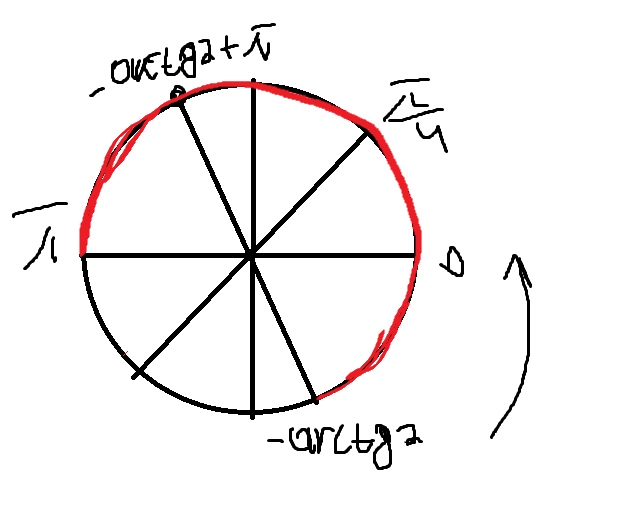
Ответ: а) \( x=-acrtg2+\pi n \),\( x=\frac{\pi}{4}+\pi n \) б) \( x=\frac{\pi}{4},-acrtg2+\pi \)
