а) Решите уравнение \( |2tgx-5|-|2tgx-1|=2 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-pi/2;pi/2]
Решение
Пусть \( tgx=t \)
Самый тупой, но проверенный способ – это рассмотреть 4 случая
- \( t>=\frac{2}{5},t>=\frac{1}{2} \) Тогда уравнение \( 2t-5-(2t-1)=2 \) – нет решений
- \( t<\frac{5}{2},t>=\frac{1}{2} \). Тогда уравнение \( -(2t-5)-(2t-1)=2 \) – откуда \( t=1 \)
- \( t>=\frac{5}{2},t>\frac{1}{2} \). Тогда уравнение \( 2t-5-(-(2t-1))=2 \) – откуда \( t=2 \) – но она не подходит под \( t>=\frac{5}{2},t>\frac{1}{2} \) значит тоже нет корней:)
- \( t<\frac{5}{2},t<\frac{1}{2} \). Тогда уравнение \( -(2t-5)-(-(2t-1))=2 \) – нет решений
Значит получаем, что \( tgx=1 \)
\( x=\frac{\pi}{4}+\pi n \)
Б) Легко отобрать на тригонометрической окружности
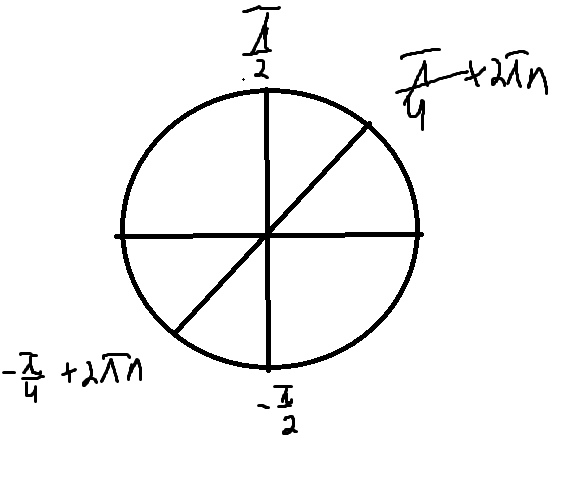
\( x=\frac{\pi}{4} \)
Ответ: а) \( x=\frac{\pi}{4}+\pi n \) б) \( x=\frac{\pi}{4} \)
