а) Решите уравнение \( log_{2}(sin(x+\frac{5\pi}{12}))+log_{2}(sin(x+\frac{\pi}{12}))=-1 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-pi;0,5pi]
Решение
Ограничения
\( sin(x+\frac{\pi}{12})>0 \) и \( sin(x+\frac{5\pi}{12})>0 \)
\( 2\pi n<x+\frac{\pi}{12}<\pi +2\pi n \)
\( 2\pi n<x+\frac{5\pi}{12}<\pi +2\pi n \)
\( -\frac{\pi}{12}+2\pi n<x<\frac{11\pi}{12}+2\pi n \)
\( -\frac{5\pi}{12}+2\pi n<x<\frac{7\pi}{12}+2\pi n \)
Решаем само уравнение
\( sin(x+\frac{5\pi}{12})*sin(x+\frac{\pi}{12})=0,5 \) Воспользуемся формулой
\( sin(t)*sin(s)=0,5*(cos(t-s)-cos(t+s)) \)
\( \frac{1}{4}+\frac{sin2x}{2}=0,5 \)
\( sin2x=0,5 \)
\( x=\frac{\pi}{12}+\pi n \)
\( x=\frac{5\pi}{12}+\pi n \)
Вспоминаем про ограничения
\( x=\frac{\pi}{12}+2\pi n \)
\( x=\frac{5\pi}{12}+2\pi n \)
б) Легче отобрать на тригонометрической окружности
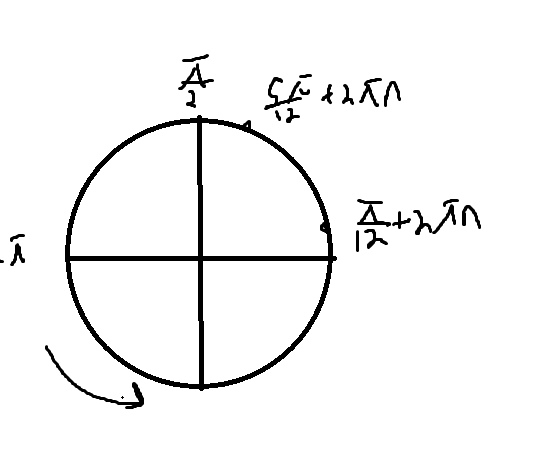
\( x=\frac{\pi}{12} \)
\( x=\frac{5\pi}{12} \)
Ответ: а) \( x=\frac{\pi}{12}+2\pi n \),\( x=\frac{5\pi}{12}+2\pi n \) б) \( x=\frac{\pi}{12}, \frac{5\pi}{12} \)
