а) Решите уравнение \( \frac{1+2sin^2x-3\sqrt{2}sinx+sin2x}{2sinx*cosx-1}=1 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-pi;pi/2]
Решение
Ограничения: \( sin2x≠1 \)
\( 2x≠\frac{\pi}{2}+2\pi n \)
\( x≠\frac{\pi}{4}+\pi n \)
Умножаем уравнение на sin2x-1
\( 1+2sin^2x-3\sqrt{2}sinx+sin2x=sin2x-1 \)
Пусть \( sinx=t \), где \( -1<=t<=1 \)
Решаем квадратное уравнение
\( t=\frac{1}{\sqrt{2}} \)
\( t=\sqrt{2} \) – не подходит по условию
\( sinx=\frac{\sqrt{2}}{2} \)
\( x=\frac{\pi}{4}+2\pi n \)
\( x=\frac{3\pi}{4}+2\pi n \)
Помним про \( x≠\frac{\pi}{4}+\pi n \)
Значит остается только \( x=\frac{3\pi}{4}+2\pi n \)
б) Легко отобрать с помощью тригонометрической окружности.
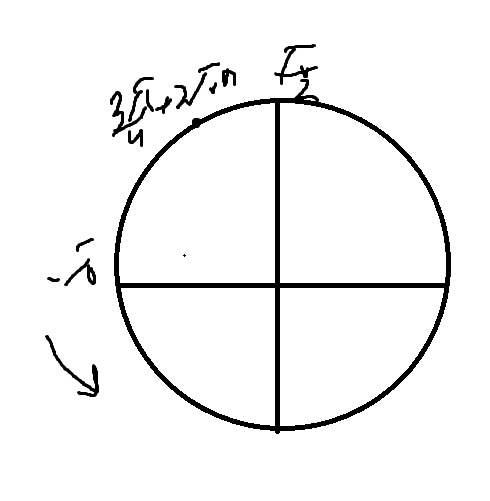
Получаем, что нет корней
Ответ: а) \( x=\frac{3\pi}{4}+2\pi n \) б) Нет корней
