а) Решите уравнение \( \sqrt{sinx*cosx}=cosx \)
б) Укажите корни этого уравнения, принадлежащие отрезку [0,5pi;2,5pi]
Решение
Ограничения \( cosx>=0 \) – это 1 и 4 четверть.
\( sinx*cosx=cos^2x \)
\( cosx(cosx-sinx)=0 \)
\( cosx=0 \) значит \( x=\frac{\pi}{2}+\pi n \)
\( cosx=sinx \) здесь мы на cosx не имеем права делить, т.к он равен нулю по условию, значит делим на sinx≠0
\( ctgx=1 \)
\( x=\frac{\pi}{4}+\pi n \), но смотрим ограничения и убираем одну точку в 3 четверти
\( x=\frac{\pi}{4}+2\pi n \)
б) Легко отобрать корни с помощью тригонометрической окружности
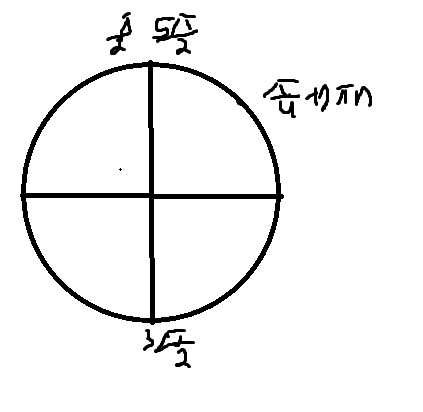
\( x=\frac{\pi}{2},\frac{3\pi}{2},\frac{9\pi}{4},\frac{5\pi}{2} \)
Ответ: а) \( x=\frac{\pi}{2}+\pi n \) , \( x=\frac{\pi}{4}+2\pi n \)
б) \( x=\frac{\pi}{2},\frac{3\pi}{2},\frac{9\pi}{4},\frac{5\pi}{2} \)
