а) Решите уравнение \( tgx*sin^2x=tgx \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-2pi/7;13pi/11]
Решение
\( tgx(sin^2x-1)=0 \)
\( tgx(sinx-1)(sinx+1)=0 \)
\( x=\pi n \) и не забываем, про \( cosx≠0,x≠\frac{\pi}{2}+\pi n \)
\( sinx=1 \) и \( sinx=-1 \) значит \( x=\frac{\pi}{2}+\pi n \) -эту серию корней мы выкидываем, т.к они не подходят под наши ограничения
Значит \( x=\pi n \)
б) Легко отобрать на тригонометрической окружности
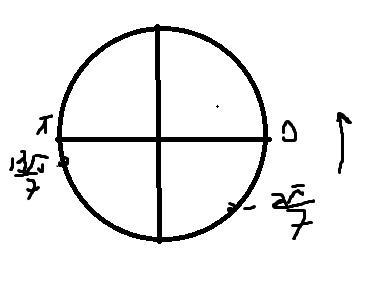
\( x=0,\pi \)
Ответ: а) \( x=\pi n \) б) \( x=0,\pi \)
