а) Решите уравнение \( 4cos^2x+2(\sqrt{2}-1)sin(\frac{\pi}{2}-x)-\sqrt{2}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [0,5pi;2pi]
Решение
Воспользуемся формулами приведения
\( 4cos^2x+2(\sqrt{2}-1)cosx-\sqrt{2}=0 \)
Делаем замену на \( cosx=t \) , \( -1≤t≤1 \)
\( 4t^2+2(\sqrt{2}-1)t-\sqrt{2}=0 \)
\( t_{1,2}=\frac{-2(\sqrt{2}-1)±\sqrt{12+8\sqrt{2}}}{8} \)
\( t_{1,2}=\frac{-2\sqrt{2}+2±\sqrt{(2+2\sqrt{2})^2}}{8} \)
\( t_{1}=-\frac{-\sqrt{2}}{2} \)
\( t_{2}=\frac{1}{2} \)
Обратная замена
\( cosx=-\frac{-\sqrt{2}}{2} \)
\( cosx=\frac{1}{2} \)
Значит
\( x=±\frac{3\pi}{4}+2 \pi n \)
\( x=±\frac{\pi}{3}+2 \pi n \)
Б) Легко отобрать с помощью тригонометрической окружности
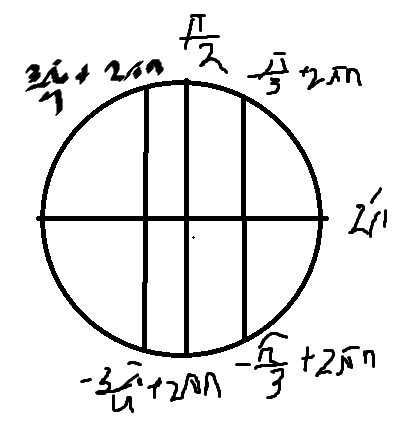
\( x=\frac{3\pi}{4} \)
\( x=\frac{5\pi}{4} \)
\( x=2\pi-\frac{\pi}{3}=\frac{5\pi}{3} \)
Ответ: а) \( x=±\frac{3\pi}{4}+2 \pi n \),\( x=±\frac{\pi}{3}+2 \pi n \)
б) \( x=\frac{3\pi}{4},\frac{5\pi}{4},\frac{5\pi}{3} \)
