а) Решите уравнение \( (\sqrt{2}^{sin^2x+\sqrt{cosx}})^2+2^{cos^2x+\sqrt{cosx}}=3*2^{\sqrt{cosx}} \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-5,5pi;-4pi]
Решение
Ограничения: \( cosx≥0 \)
\( 2^{sin^2x+\sqrt{cosx}}+2^{cos^2x+\sqrt{cosx}}=3*2^{\sqrt{cosx}} \)
\( 2^{\sqrt{cosx}}(2^{sin^2x}+2^{cos^2x}-3)=0 \)
\( 2^{cosx}(2^{sin^2x}+2^{1-sin^2x}-3)=0 \)
\( 2^{\sqrt{cosx}}=0 \) – нет решений, т.к показательная функция всегда строго больше нуля.
или
\( 2^{sin^2x}+2^{1-sin^2x}-3=0 \)
сделаем замену на \( 2^{sin^2x}=t \), \( t>0 \)
\( t+\frac{2}{t}-3=0 \) – смело умножаем все на t
\( t^2-3t+2=0 \)
\( t=1 \)
\( t=2 \)
Обратная замена
\( 2^{sin^2x}=1 \)
\( 2^{sin^2x}=2 \)
Получаем
\( sin^2x=0 \)
\( sin^2x=1 \)
Значит
\( sinx=0 \)
\( sinx=1 \)
\( sinx=-1 \)
Тогда
\( x=\pi n \)
\( x=\frac{\pi}{2}+2\pi n \)
\( x=-\frac{\pi}{2}+2\pi n \)
Объединим две серии в одну
\( x=\pi n \) – тут не все точки удовлетворяют нашему ограничению
\( x=\frac{\pi}{2}+\pi n \)
Так как cos положителен в 1 и 4 четверти, то ответ перепишется в следующем виде
\( x=2\pi n \)
\( x=\frac{\pi}{2}+\pi n \)
Б) Легко отобрать на тригонометрической окружности
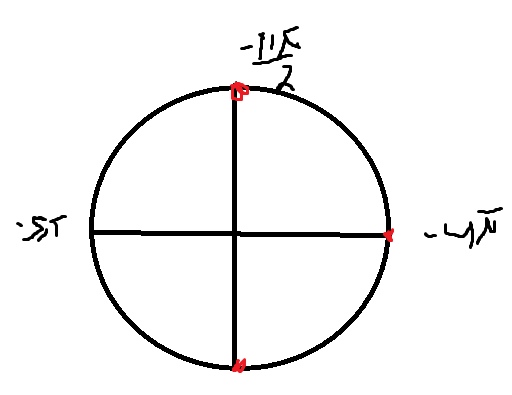
\( x=-\frac{11\pi}{2} \)
\( x=-\frac{9\pi}{2} \)
\( x=-4\pi \)
Ответ: а) \( x=2\pi n \) ,\( x=\frac{\pi}{2}+\pi n \) б)\( x=-\frac{11\pi}{2} \),\( x=-\frac{9\pi}{2} \),
\( x=-4\pi \)
