а) Решите уравнение \( log_{3-4cos^2x}(9-16cos^4x)=2+\frac{1}{log_{2}(3-4cos^2x)} \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-pi/3;2pi/3]
Решение
ОДЗ:
\( cosx≠±\frac{\sqrt{3}}{2} \)
\( 3-4cos^2x>0 \)
\( 3-4cos^2x≠1 \)
Решаем само уравнение
\( log_{3-4cos^2x}(3-4cos^2x)(3+4cos^2x)=2+log_{3-4cos^2x}(2) \)
\( 1+log_{3-4cos^2x}(3+4cos^2x)=2+log_{3-4cos^2x}(2) \)
\( log_{3-4cos^2x}(\frac{3+4cos^2x}{2})=1 \)
\( 3+4cos^2x=6-8cos^2x \)
\( cosx=±\frac{1}{2} \) – под ОДЗ подходит
\( x=±\frac{\pi}{3}+\pi n \)
Б) Легко отобрать с помощью окружности
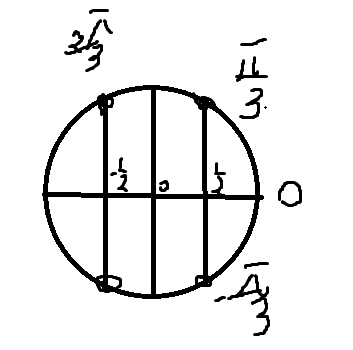
\( x=-\frac{\pi}{3},\frac{\pi}{3},\frac{2\pi}{3} \)
Ответ: а) \( x=±\frac{\pi}{3}+\pi n \) б) \( x=-\frac{\pi}{3},\frac{\pi}{3},\frac{2\pi}{3} \)
