а) Решите уравнение \( (32^{cosx})^{sinx}=4\sqrt{2} \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-4,5pi;-3pi]
Решение
а) \( 2^{5sinx*cosx}=2^{\frac{5}{2}} \)
\( 5sinx*cosx=\frac{5}{2} \)
\( 2sinx*cosx=1 \)
\( sin2x=1 \)
\( 2x=\frac{\pi}{2}+2\pi n \)
\( x=\frac{\pi}{4}+\pi n \)
б) Легко отобрать с помощью окружности
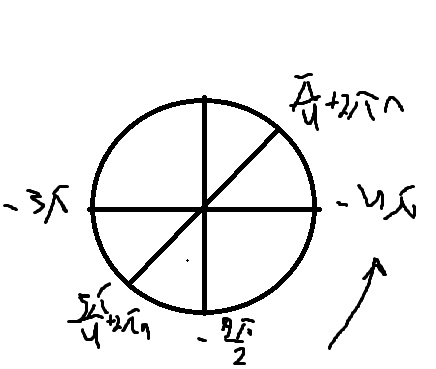
\( x=-4\pi+\frac{\pi}{4}=-\frac{15 \pi}{4} \)
Ответ: а)\( x=\frac{\pi}{4}+\pi n \),б) \( x=-\frac{15 \pi}{4} \)
