а) Решите уравнение \( \frac{3^{cos^2x}+3^{sin^2x}-4}{sinx+1}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [5,5pi;7pi]
Решение
ОДЗ \( sinx≠-1 \)
\( \frac{3^{1-sin^2x}+3^{sin^2x}-4}{sinx+1}=0 \)
Пусть \( 3^{sin^2x}=t,t>0 \)
\( \frac{3}{t}+t-4=0 \)
\( t^2-4t+3=0 \)
\( (t-1)(t-3)=0 \)
Обратная замена
\( 3^{sin^2x}=1 \), \( sinx=0 \)
\( 3^{sin^2x}=3 \), \( sinx=±1 \)
В итоге нам подходит, только \( sinx=0 \), \( sinx=1 \)
\( x=\pi n \)
\( x=\frac{\pi}{2}+2 \pi n \)
Б) Легче всего отобрать на окружности
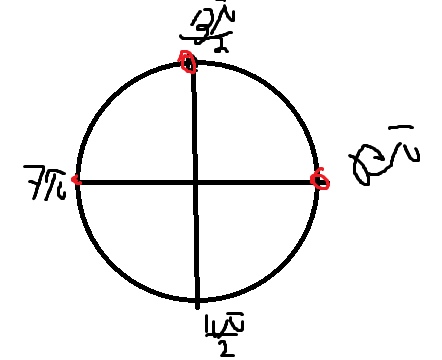
Ответ: а) \( x=\pi n \), \( x=\frac{\pi}{2}+2 \pi n \) б) \( x=6 \pi,\frac{13 \pi}{2},7 \pi \)
