а) Решите уравнение \( sin2x+\sqrt{2cosx-2cos^3x}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку [-pi,-pi/6]
Решение
ОДЗ: \( sin2x≤0 \) – это 2 и 4 четверть на тригонометрической окружности
Возведем обе части в квадрат
\( (2sinx*cosx)^2=2cosx-2cos^3x \)
\( 4cos^2x*(1-cos^2x)=2cosx-cos^3x \)
Пусть \( cosx=t \), где \( -1≤t≤1 \)
\( 4t^2(1-t^2)=2t-2t^3 \)
\( (1-t^2)(2t^2-t)=0 \)
\( (t+1)(t-1)(2t-1)t=0 \)
Делаем обратную замену
\( cosx=-1 \) значит \( x=\pi+2 \pi n \)
\( cosx=0 \) значит \( x=\frac{\pi }{2}+\pi n \)
\( cosx=1 \) значит \( x=2 \pi n \)
\( cosx=0,5 \) значит \( x=±\frac{\pi }{3}+2\pi n \)
По ОДЗ нам подходит только
\( x=\pi+2 \pi n \), \( x=\frac{\pi }{2}+\pi n \), \( x=2 \pi n \), \( x=-\frac{\pi }{3}+2\pi n \)
Б)
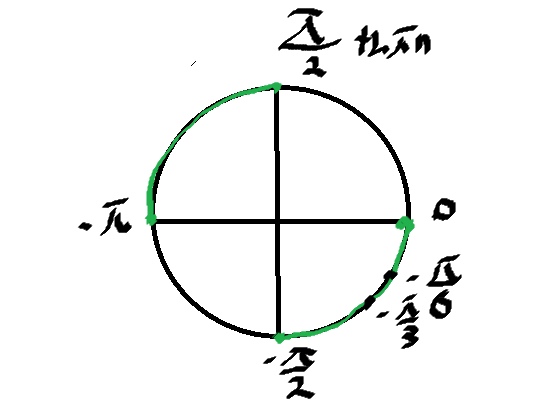
\( x=-\pi,-\frac{\pi}{2},-\frac{\pi}{3} \)
Ответ: а)\( x=\pi+2 \pi n \),\( x=\frac{\pi }{2}+\pi n \), \( x=2 \pi n \) , \( x=-\frac{\pi }{3}+2\pi n \)
б) \( x=-\pi,-\frac{\pi}{2},-\frac{\pi}{3} \)
P.S Если понравилось решение или что-то не было понятно, то пиши комментарий ниже, мне будет приятно:)
